题目内容
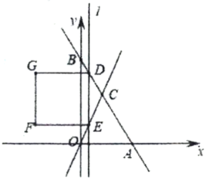
【题目】如图,正方形ABCD的边长为3,且∠EDF=45°,将△DAE绕点D逆时针旋转90°,得到△DCM.若AE=1,则FM的长为______

【答案】![]()
【解析】由旋转可得DE=DM,∠EDM为直角,可得出∠EDF+∠MDF=90°,由∠EDF=45°,得到∠MDF为45°,可得出∠EDF=∠MDF,再由DF=DF,利用SAS可得出三角形DEF与三角形MDF全等,由全等三角形的对应边相等可得出EF=MF;则可得到AE=CM=1,正方形的边长为3,用AB﹣AE求出EB的长,再由BC+CM求出BM的长,设EF=MF=x,可得出BF=BM﹣FM=BM﹣EF=4﹣x,在直角三角形BEF中,利用勾股定理列出关于x的方程,求出方程的解得到x的值,即为FM的长.
解:∵△DAE逆时针旋转90°得到△DCM,
∴∠FCM=∠FCD+∠DCM=180°,
∴F、C、M三点共线,
∴DE=DM,∠EDM=90°,
∴∠EDF+∠FDM=90°,
∵∠EDF=45°,
∴∠FDM=∠EDF=45°,
在△DEF和△DMF中,
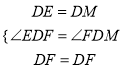 ,
,
∴△DEF≌△DMF(SAS),
∴EF=MF,
设EF=MF=x,
∵AE=CM=1,且BC=3,
∴BM=BC+CM=3+1=4,
∴BF=BM﹣MF=BM﹣EF=4﹣x,
∵EB=AB﹣AE=3﹣1=2,
在Rt△EBF中,由勾股定理得EB2+BF2=EF2,
即22+(4﹣x)2=x2,
解得:x=![]() ,
,
∴FM=![]() .
.
故答案为: ![]() .
.

 阅读快车系列答案
阅读快车系列答案【题目】小明到某服装专卖店去做社会调查,了解到该专卖店为了激励营业员的工作积极性,实行“月总收入=基本工资+计件奖金”的方法计算薪资,并获得如下信息:
营业员 | 小张 | 小王 |
月销售件数 | 200 | 150 |
月总收入/元 | 1400 | 1250 |
假设月销售件数为x,月总收入为y元,销售每件奖励a元,营业员月基本工资为b元.
(1)求a、b的值.
(2)若营业员小张上个月总收入是1700元,则小张上个月卖了多少件服装?