题目内容
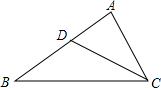
如图，已知△ABC中CE⊥AB于E，BF⊥AC于F．求证：（1）△ABF∽△ACE；（2）△AEF∽△ACB．
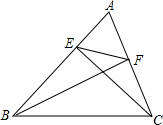
证明：（1）∵CE⊥AB于E，BF⊥AC于F，
∴∠AFB=∠AEC，∠A为公共角，
∴△ABF∽△ACE（两角对应相等的两个三角形相似）．
（2）由（1）得AB：AC=AF：AE，∠A为公共角，
∴△AEF∽△ACB（两边对应成比例且夹角相等的两个三角形相似）．
∴∠AFB=∠AEC，∠A为公共角，
∴△ABF∽△ACE（两角对应相等的两个三角形相似）．
（2）由（1）得AB：AC=AF：AE，∠A为公共角，
∴△AEF∽△ACB（两边对应成比例且夹角相等的两个三角形相似）．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
