题目内容
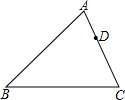
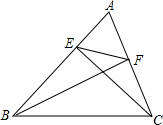
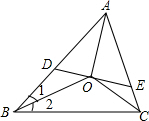
如图,△ABC三内角平分线交于点D,过点D引DE⊥AO,分别交AB、AC于点D、E.求证:△BOD∽△BCO∽△OCE.
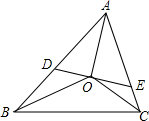

证明:∵AO平分∠BAC,DE⊥AO,
∴∠DAO=∠EAO.
在△ADO和△AEO中,
,
∴△ADO≌△AEO(ASA),
∴∠ADO=∠AEO,
∴∠BDO=∠OEC=90°+
∠BAC,
∴∠BOC=90°+
∠BAC,
∴∠BDO=∠OEC=∠BOC,
∵O是△ABC的内角平分线的交点,
∴∠1=∠2,
∴△DBO∽△OBC,
同理可得出:△BOC∽△OEC,
∴△DBO∽△EOC,
∴△BOD∽△BCO∽△OCE.
∴∠DAO=∠EAO.
在△ADO和△AEO中,
|
∴△ADO≌△AEO(ASA),
∴∠ADO=∠AEO,
∴∠BDO=∠OEC=90°+
| 1 |
| 2 |
∴∠BOC=90°+
| 1 |
| 2 |
∴∠BDO=∠OEC=∠BOC,
∵O是△ABC的内角平分线的交点,
∴∠1=∠2,
∴△DBO∽△OBC,
同理可得出:△BOC∽△OEC,
∴△DBO∽△EOC,
∴△BOD∽△BCO∽△OCE.


练习册系列答案
相关题目