题目内容
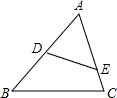
已知：△ABC中，∠A=36°，AB=AC，BD平分∠ABC交AC于点O，试说明：△BDC∽△ABC．
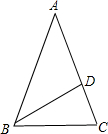
∵AB=AC，∴∠ABC=∠C=
=72°，
∵BD为∠ABC的角平分线，
∴∠CBD=
=36°，
∴∠CBD=∠A，又∵∠C=∠C，
∴△BDC∽△ABC．
| 180°-36° |
| 2 |
∵BD为∠ABC的角平分线，
∴∠CBD=
| ∠ABC |
| 2 |
∴∠CBD=∠A，又∵∠C=∠C，
∴△BDC∽△ABC．
练习册系列答案
名校课堂系列答案
相关题目
