��Ŀ����
����Ŀ����ͼ����ƽ��ֱ�DZ�ϵ�У���ABC��������������ΪA��-3��1����B��-4��-3����C��-2��-4������ABC��ԭ��˳ʱ����ת180�����õ���A1B1C1�ٽ���A1B1C1����ƽ��5����λ�õ���A2B2C2��
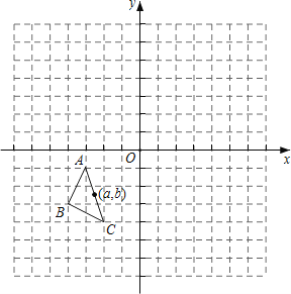
��1��������A1B1C1����д����A�Ķ�Ӧ��A1�����ꣻ
��2��������A2B2C2����д����A�Ķ�Ӧ��A2�����ꣻ
��3��P��a��b������ABC�ı�AC��һ�㣬��ABC����ת��ƽ�ƺ��P�Ķ�Ӧ��ֱ�ΪP1��P2����ֱ��д����P2�����꣮
���𰸡���1����ͼ����A1B1C1Ϊ����������������A�Ķ�Ӧ��A1������Ϊ��3��1������2����ͼ����A2B2C2Ϊ����������������A�Ķ�Ӧ��A2������Ϊ��-2��1������3��P2������Ϊ��-a-5��-b����
��������
��1���������⣬�ֱ��ҳ���A��B��C����ԭ��ĶԳƵ�A1��B1��C1��Ȼ������A1B1��A1C1��B1C1���ɣ�Ȼ����ݹ���ԭ��ԳƵ����������ϵ�������������Ϊ�෴�����ɵó����ۣ�
��2���ֱ�A1��B1��C1����ƽ��5����λ�õ�A2��B2��C2��Ȼ������A2B2��A2C2��B2C2���ɣ�Ȼ����ݵ������ƽ�ƹ��ɣ�����������Ҽӣ��������ϼ��¼������ɵó����ۣ�
��3���ȸ��ݹ���ԭ��ԳƵ����������ϵ�������������Ϊ�෴���������P1�����꣬Ȼ����ݵ������ƽ�ƹ��ɣ�����������Ҽӣ��������ϼ��¼����������P2������
��1���ֱ��ҳ���A��B��C����ԭ��ĶԳƵ�A1��B1��C1��Ȼ������A1B1��A1C1��B1C1����ͼ����A1B1C1Ϊ��������A�Ķ�Ӧ��A1������Ϊ��3��1����
��2���ֱ�A1��B1��C1����ƽ��5����λ�õ�A2��B2��C2��Ȼ������A2B2��A2C2��B2C2����ͼ����A2B2C2Ϊ��������A�Ķ�Ӧ��A2������Ϊ��-2��1����

��3��P��a��b��������ת�õ��Ķ�Ӧ��P1������Ϊ��-a��-b������P1ƽ�Ƶõ���Ӧ��P2������Ϊ��-a-5��-b����