题目内容
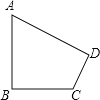
【题目】已知:如图,∠B=∠D=90°,∠A=60°,AB=4,CD=2.求:四边形ABCD的面积.
【答案】6![]() .
.
【解析】
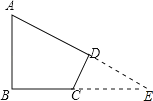
试题分析:延长AD,BC,交于点E,在直角三角形ABE中,利用30度角所对的直角边得到AE=2AB,再利用勾股定理求出BE的长,在直角三角形DCE中,同理求出DE的长,四边形ABCD面积=三角形ABE面积﹣三角形DCE面积,求出即可.
解:延长AD,BC,交于点E,
在Rt△ABE中,∠A=60°,AB=4,
∴∠E=30°,AE=2AB=8,
∴BE=![]() =4
=4![]() ,
,
在Rt△DCE中,∠E=30°,CD=2,
∴CE=2CD=4,根据勾股定理得:DE=![]() =2
=2![]() ,
,
则S四边形ABCD=S△ABE﹣S△DCE=![]() ABBE﹣
ABBE﹣![]() DCED=8
DCED=8![]() ﹣2
﹣2![]() =6
=6![]() .
.

练习册系列答案
相关题目
【题目】在平面直角坐标系中,点P的横坐标是-3,且点P到x轴的距离为5,则P的坐标是( )
A. (-3,5)或(-3,-5) B. (5,-3)或(-5,-3)
C. (-3,5) D. (-3,-3)