题目内容
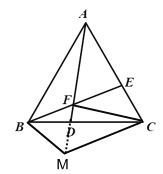
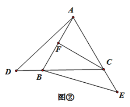
【题目】如图,△ABC是等边三角形,点D、E分别是直线BC、AC上的点,且BD=CE.
(1)如图①,当点D、E分别在线段BC、AC上时,BE与AD相交于点F.求∠AFB的度数.
(2)如图②,当点D在CB的延长线上,点E在AC的延长线上时,CF为△ABC的高线则线段CD、AF、CE、之间的数量关系是 ,并加以证明.
(3)在①的条件下,连接FC,如图③,若∠DFC=90°,AF= 3![]() ,求BF的长.
,求BF的长.


【答案】(1)120°;(2) ![]() ;(3)
;(3)![]() .
.
【解析】
(1)根据等边三角形的性质直接利用SAS证明△ABD≌△BCE,得到∠BAD=∠CBE,然后根据三角形内角和定理可求∠AFB的度数;
(2)根据等边三角形的性质直接利用SAS证明△ABD≌△BCE,得到BD=CE,然后根据等边三角形三线合一的性质可得BC=2AF,易得CD=BC+BD=2AF+CE;
(3)将△ABF绕点B顺时针旋转60°得到△CBM,连接FM,根据旋转的性质可得△BMF为等边三角形,求出A、F、M三点共线,∠FMC=60°,结合∠DFC=90°,利用含30度直角三角形的性质可求出MF,然后可得BF.
解:(1)∵△ABC是等边三角形,
∴AB=BC,∠ABD=∠BCE,
∵BD=CE,
∴△ABD≌△BCE(SAS),
∴∠BAD=∠CBE,
∵∠AFB+∠BAD+∠ABF=180°,
∴∠AFB+∠CBE+∠ABF=180°,
∵∠CBE+∠ABF=∠ABC=60°,
∴∠AFB=120°;
(2)∵△ABC是等边三角形,
∴AB=BC,∠ABC=∠ACB,
∴∠ABD=∠BCE,
∵BD=CE,
∴△ABD≌△BCE(SAS),
∴BD=CE,
∵CF为△ABC的高线,
∴AB=2AF,即BC=2AF,
∴CD=BC+BD=2AF+CE;
(3)如图,将△ABF绕点B顺时针旋转60°得到△CBM,连接FM,
则BF=BM,∠FBM=60°,
∴△BMF为等边三角形,
∴∠BFM=60°,
∵∠AFB=120°,
∴A、F、M三点共线,∠BMC=∠AFB=120°,
∴∠FMC=∠BMC-∠BMF=120°-60°=60°,
∵∠DFC=90°,AF=![]() ,
,
∴MC=AF=![]() ,
,
∴![]() ,
,
∴![]() .
.