题目内容
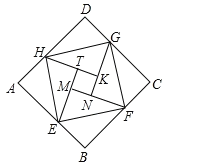
【题目】如图，已知四边形ABCD是边长为4的正方形，E为AB的中点，将△ADE绕点D沿逆时针方向旋转后得到△DCF，连接EF，则EF的长为（ ）
A. 2
B. 2
C. 2
D. 2
【答案】D
【解析】
先利用勾股定理计算出DE，再根据旋转的性质得∠EDF=∠ADC=90°，DE=DF，则可判断△DEF为等腰直角三角形，然后根据等腰直角三角形的性质计算EF的长．
∵E为AB的中点，AB=4，∴AE=2，
∴DE=
=2
．
∵四边形ABCD为正方形，∴∠A=∠ADC=90°，∴∠ADE+∠EDC=90°．
∵△ADE绕点D沿逆时针方向旋转后得到△DCF，∴∠ADE=∠CDF，DE=DF，∴∠CDF+∠EDC=90°，∴△DEF为等腰直角三角形，∴EF=
DE=2
．
故选D．
练习册系列答案
相关题目
