Question

【题目】直角三角形斜边上的中线把直角三角形分成的两个三角形的关系是（　　）

A. 形状相同 B. 周长相等 C. 面积相等 D. 全等

Answer 1

【答案】C

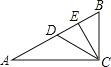
【解析】画出图形，逐项分析即可得；A、题目已知条件不能证明△ACD与△CDB的形状相同；B、又AC≠BC，所以△ACD与△CDB的周长不等；C、如图，在直角△ABC中，∠ACB=90°，CD是斜边AB上的中线，CE是AB上的高，根据直角三角形的性质可以推CD=AD=BD，再根据三角形的面积公式可以得到S△ACD=S△CBD；D、此题可根据直角三角形的性质结合全等三角形的判定方法进行判断．

如图，A、显然△ACD与△CDB的形状不同，故A不正确；

B、∵AC≠BC，∴△ACD与△CDB的周长不等，故B不正确；

C、在直角△ABC中，∠ACB=90°，CD是斜边AB上的中线，CE是AB上的高，

根据直角三角形中斜边上的中线等于斜边的一半知，CD=AD=BD，

∴S△ACD=ADCE=BDCE=S△CBD，故C正确；

D、由于AD=CD=BD，所以∠A=∠DCA，∠B=∠DCB，

显然∠A、∠B不一定相等，因此两个三角形不全等，故D错误，

故选C．