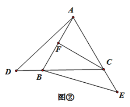
题目内容
【题目】已知,如图:AD是△ABC的中线,AE⊥AB,AE=AB,AF⊥AC,AF=AC,连结EF.试猜想线段AD与EF的关系,并证明

【答案】EF=2AD,EF⊥AD;证明见解析
【解析】
先猜想EF=2AD,EF⊥AD.延长AD到M,使得AD=DM,连接MC,延长DA交EF于N,易证BD=CD,即可证明△ABD≌△MCD,可得AB=MC,∠BAD=∠M,即可求得∠EAF=∠MCA,即可证明△AEF≌△CMA,可得EF=AM,∠CAM=∠F,即可解题.
猜想:EF=2AD,EF⊥AD.
证明:如图,延长AD到M,使得AD=DM,连接MC,延长DA交EF于N,
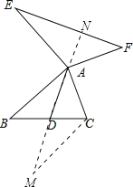
∴AD=DM,AM=2AD,
∵AD是△ABC的中线,∴BD=CD,
在△ABD和△MCD中,
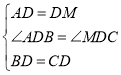 , ∴△ABD≌△MCD(SAS),
, ∴△ABD≌△MCD(SAS),
∴AB=MC,∠BAD=∠M,
∵AB=AE,∴AE=MC,
∵AE⊥AB,AF⊥AC,∴∠EAB=∠FAC=90°,
∵∠FAC+∠BAC+∠EAB+∠EAF=360°,∴∠BAC+∠EAF=180°,
∵∠CAD+∠M+∠MCA=180°,∴∠CAD+∠BAD+∠MCA=180°,
即∠BAC+∠MCA=180°,∴∠EAF=∠MCA.
在△AEF和△CMA中,
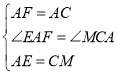 ,∴△AEF≌△CMA(SAS),
,∴△AEF≌△CMA(SAS),
∴EF=AM,∠CAM=∠F,∴EF=2AD;
∵∠CAF=90°,∴∠CAM+∠FAN=90°,
∵∠CAM=∠F,∴∠F+∠FAN=90°,
∴∠ANF=90°,∴EF⊥AD.

练习册系列答案
相关题目