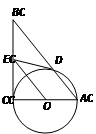题目内容
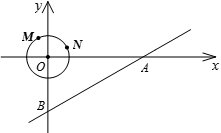
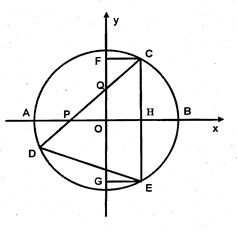
如图,在直角坐标系中,⊙O的圆心O在坐标原点,直径AB=8,点P是直径AB上的一个动点(点P不与A、B两点重合),过点P的直线PQ的解析式为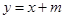 ,当直线PQ交y轴于Q,交⊙O于C、D两点时,过点C作CE垂直于x轴交⊙O于点E,过点E作EG垂直于y轴,垂足为G,过点C作CF垂直于y轴,垂足为F,连接DE.
,当直线PQ交y轴于Q,交⊙O于C、D两点时,过点C作CE垂直于x轴交⊙O于点E,过点E作EG垂直于y轴,垂足为G,过点C作CF垂直于y轴,垂足为F,连接DE.
(1)点P在运动过程中,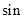 ∠CPB= ;
∠CPB= ;
(2)当m=3时,试求矩形CEGF的面积;
(3)当P在运动过程中,探索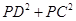 的值是否会发生变化?如果发生变化,请你说明理由;如果不发生变化,请你求出这个不变的值;
的值是否会发生变化?如果发生变化,请你说明理由;如果不发生变化,请你求出这个不变的值;
(4)如果点P在射线AB上运动,当△PDE的面积为4时,请你求出CD的长度
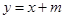 ,当直线PQ交y轴于Q,交⊙O于C、D两点时,过点C作CE垂直于x轴交⊙O于点E,过点E作EG垂直于y轴,垂足为G,过点C作CF垂直于y轴,垂足为F,连接DE.
,当直线PQ交y轴于Q,交⊙O于C、D两点时,过点C作CE垂直于x轴交⊙O于点E,过点E作EG垂直于y轴,垂足为G,过点C作CF垂直于y轴,垂足为F,连接DE.
(1)点P在运动过程中,
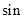 ∠CPB= ;
∠CPB= ;(2)当m=3时,试求矩形CEGF的面积;
(3)当P在运动过程中,探索
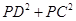 的值是否会发生变化?如果发生变化,请你说明理由;如果不发生变化,请你求出这个不变的值;
的值是否会发生变化?如果发生变化,请你说明理由;如果不发生变化,请你求出这个不变的值;(4)如果点P在射线AB上运动,当△PDE的面积为4时,请你求出CD的长度
(1)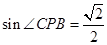
(2)7
(3)不变
(4)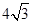 或4
或4
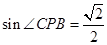
(2)7
(3)不变
(4)
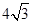 或4
或4(1)由直线PQ的解析式y=x+m,可知直线与x轴的交点为(-m,0),与y轴的交点是(0,m),所以QO=PO,角CPB等于45 即
即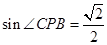
(2)∵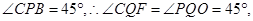

则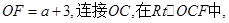
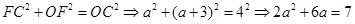
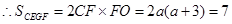
(3)∵AB垂直平分CE,∴PC=PE,且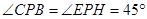 ,
,
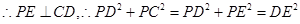
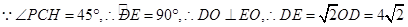
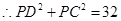
(4)当点P在直径AB上时,
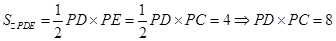
又
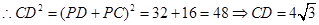
当点P在AB延长线上,
同理可得:
 即
即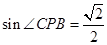
(2)∵
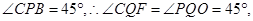

则
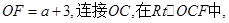
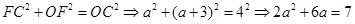
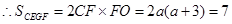
(3)∵AB垂直平分CE,∴PC=PE,且
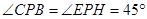 ,
,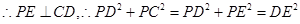
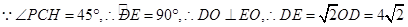
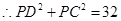
(4)当点P在直径AB上时,
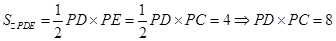
又

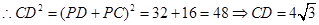
当点P在AB延长线上,
同理可得:


练习册系列答案
相关题目
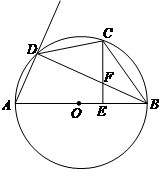
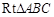 中,
中,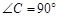 ,以AC为直径作
,以AC为直径作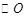 ,交AB于D,过O作OE//AB,交BC于E,求证:ED为
,交AB于D,过O作OE//AB,交BC于E,求证:ED为