题目内容
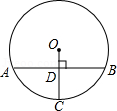
图,有一直径为4的圆形铁皮,要从中剪出一个最大圆心角为60°的扇形ABC.那么剪下的扇形ABC(阴影部分)的面积为 ;用此剪下的扇形铁皮围成一个圆锥,该圆锥的底面圆的半径r= .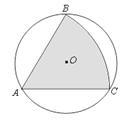

2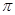 ;
;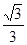
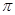 ;
;
连接OA,过点O作OD⊥AB,
∵∠CAB=60°,
∴∠OAD=30°,
∵AO=2,
∴DO=1,
∴AD=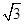 ,
,
∴AB=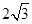 ,
,
∴S阴影=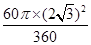 =2π,
=2π,
∵S阴影=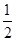 ×弧长×
×弧长×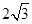 ,
,
∴弧长=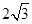 /3 π,
/3 π,
∴弧长=2πr,
∴r=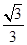 .
.
故答案为:2π;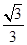 .
.
∵∠CAB=60°,
∴∠OAD=30°,
∵AO=2,
∴DO=1,
∴AD=
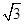 ,
,∴AB=
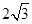 ,
,∴S阴影=
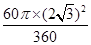 =2π,
=2π,∵S阴影=
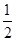 ×弧长×
×弧长×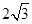 ,
,∴弧长=
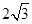 /3 π,
/3 π,∴弧长=2πr,
∴r=
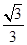 .
.故答案为:2π;
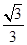 .
.
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
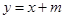 ,当直线PQ交y轴于Q,交⊙O于C、D两点时,过点C作CE垂直于x轴交⊙O于点E,过点E作EG垂直于y轴,垂足为G,过点C作CF垂直于y轴,垂足为F,连接DE.
,当直线PQ交y轴于Q,交⊙O于C、D两点时,过点C作CE垂直于x轴交⊙O于点E,过点E作EG垂直于y轴,垂足为G,过点C作CF垂直于y轴,垂足为F,连接DE.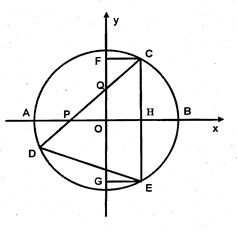
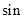 ∠CPB= ;
∠CPB= ;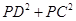 的值是否会发生变化?如果发生变化,请你说明理由;如果不发生变化,请你求出这个不变的值;
的值是否会发生变化?如果发生变化,请你说明理由;如果不发生变化,请你求出这个不变的值;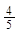 , 求线段AD的长。
, 求线段AD的长。 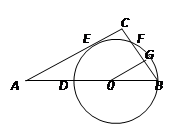
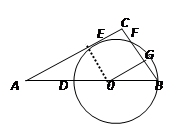
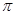
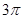
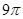
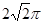
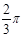
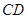 与线段
与线段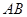 为直径的圆相切于点
为直径的圆相切于点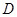 ,并交
,并交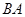 的延长线于点
的延长线于点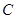 ,且
,且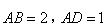 ,
,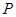 点在切线
点在切线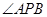 的度数最大时,则
的度数最大时,则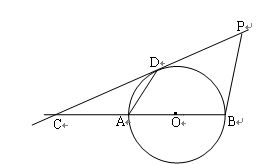
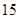 °
°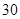 °
°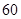 °
°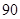 °
°