题目内容
如图，以直角坐标系的原点O作⊙O，点M、N是⊙O上的两点，M（－1，2），N（2，1）
小题1:试在x轴上找出点P使PM+PN最小，求出P的坐标；
小题2:若在坐标系中另有一直线AB，A（10，0），点B在y轴上，∠BAO=30°，⊙O以0. 2个单位/秒的速度沿x轴正方向运动，问圆在运动过程中与该直线相交的时间有多长？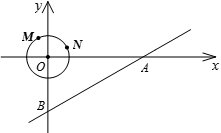
小题1:试在x轴上找出点P使PM+PN最小，求出P的坐标；
小题2:若在坐标系中另有一直线AB，A（10，0），点B在y轴上，∠BAO=30°，⊙O以0. 2个单位/秒的速度沿x轴正方向运动，问圆在运动过程中与该直线相交的时间有多长？
小题1:P（1，0）
小题2:
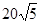秒本题考查的是圆的相关特性。
（1）得点M（－1，2）关于X轴的对称点坐标为（－1，－2）。
且在⊙O上，又∵过N（2，1）与（－1，－2）的直线为y=x-1当y=0时，x=1故P（1，0）。
（2）由题意勾股定理得当与直线相切时OA=2半径=2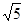
所以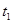
=(10-2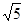)÷0.2，
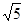=(10+2)÷0.2
所以t=-=
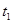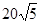
（1）得点M（－1，2）关于X轴的对称点坐标为（－1，－2）。
且在⊙O上，又∵过N（2，1）与（－1，－2）的直线为y=x-1当y=0时，x=1故P（1，0）。
（2）由题意勾股定理得当与直线相切时OA=2半径=2
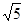
所以
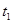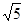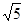=(10-2)÷0.2，=(10+2)÷0.2所以t=
-=
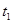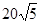
练习册系列答案
相关题目
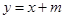，当直线PQ交y轴于Q，交⊙O于C、D两点时，过点C作CE垂直于x轴交⊙O于点E，过点E作EG垂直于y轴，垂足为G，过点C作CF垂直于y轴，垂足为F，连接DE．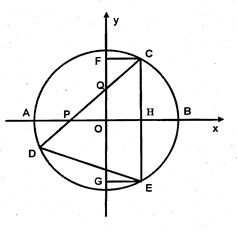
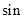∠CPB= ；
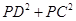的值是否会发生变化？如果发生变化，请你说明理由；如果不发生变化，请你求出这个不变的值；
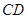与线段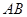
为直径的圆相切于点
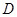，并交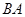
的延长线于点
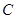，且
，
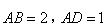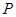点在切线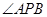
的度数最大时，则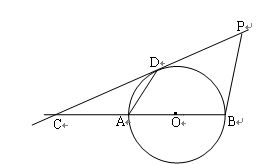
°
°
°
°
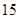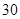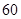