题目内容
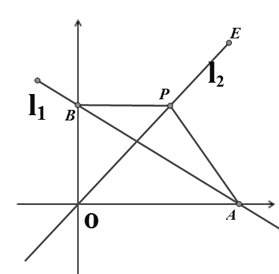
【题目】如图,在平面直角坐标系中,直线![]() :
:![]() 经过
经过![]() ,
,![]() 两点,且
两点,且![]() 、
、![]() 满足
满足![]() ,过点
,过点![]() 作
作![]() 轴,交直线
轴,交直线![]() :
:![]() 于点
于点![]() ,连接
,连接![]() .
.
(1)求直线![]() 的函数表达式;
的函数表达式;
(2)在直线![]() 上是否存在一点
上是否存在一点![]() ,使得
,使得![]() ?若存在,求出点
?若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
(3)点![]() 是
是![]() 轴上的一个动点,点
轴上的一个动点,点![]() 是
是![]() 轴上的一个动点,过点
轴上的一个动点,过点![]() 作
作![]() 轴的垂线交直线
轴的垂线交直线![]() 、
、![]() 于点
于点![]() 、
、![]() ,若
,若![]() 是等腰直角三角形,请直接写出符合条件的
是等腰直角三角形,请直接写出符合条件的![]() 的值.
的值.
【答案】(1)![]() ;(2)存在点
;(2)存在点![]() ,
,![]() 点的纵坐标为0或4;(3)4或
点的纵坐标为0或4;(3)4或![]() 或
或![]() 或
或![]() .
.
【解析】
(1)根据非负性求出a、b的值,然后运用待定系数法解答即可;
(2)根据平行和坐标以及![]() 确定Q坐标即可;
确定Q坐标即可;
(3)连接DM、DN,由题意可得M、N的坐标分别为(n,![]() ),(n,n),MN=|
),(n,n),MN=|![]() n-2|,然后再分MN=DM,MN=DN,DM=DN三种情况解答即可.
n-2|,然后再分MN=DM,MN=DN,DM=DN三种情况解答即可.
解:(1)∵![]()
∴![]()
![]()
∴![]()
![]()
把![]() 、
、![]() 代入
代入![]() 中,得:
中,得:
![]()
解得: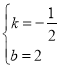
∴![]()
(2)存在点![]() ,使
,使![]() .
.
∵![]()
![]()
∴![]()
![]()
∴![]()
∵![]()
∴![]() 点的纵坐标为0或4
点的纵坐标为0或4
∴![]()
![]()
(3) ①当DM=MN或DM=DN时,如图:过M做DM∥x轴交y轴于D点,连接DN
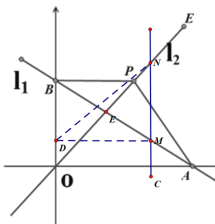
∵C点坐标为(n,n),
∴M、N的坐标分别为(n,![]() ),(n,n),D(0,n) MN=|
),(n,n),D(0,n) MN=|![]() n-2|,
n-2|,
∴|![]() n-2|=|n|,解得:n=4或n=
n-2|=|n|,解得:n=4或n=![]()
②当DM=DN或DM=DN时,如图
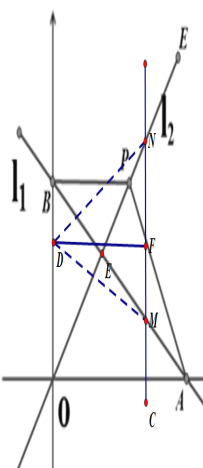
∵C点坐标为(n,n),
∴M、N的坐标分别为(n,![]() ),(n,n),D(0,n) MN=|
),(n,n),D(0,n) MN=|![]() n-2|,
n-2|,
又∵![]() 是等腰直角三角形
是等腰直角三角形
∴D在MN的垂直平分线上,DF=![]() MN
MN
∴,D(0, ![]() +1)F(n,
+1)F(n,![]() |)
|)
∴|n| =![]() |
|![]() n-2|,解得:
n-2|,解得:![]() 或
或![]()
综上,n的取值为4或![]() 或
或![]() 或
或![]() 时,
时,![]() 是等腰直角三角形.
是等腰直角三角形.

 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案【题目】某市团委举办“我的中国梦”为主题的知识竞赛,甲、乙两所学校参赛人数相等,比赛结束后,发现学生成绩分别为70分、80分、90分、100分,并根据统计数据绘制了如下不完整的统计图表:

乙校成绩统计表
分数/分 | 人数/人 |
70 | 7 |
80 | |
90 | 1 |
100 | 8 |
(1)在图①中,“80分”所在扇形的圆心角度数为________;
(2)请你将图②补充完整;
(3)求乙校成绩的平均分;
(4)经计算知s甲2=135,s乙2=175,请你根据这两个数据,对甲、乙两校成绩作出合理评价.
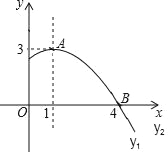
【题目】企业的污水处理有两种方式:一种是输送到污水厂进行集中处理,另一种是通过企业的自身设备进行处理.某企业去年每月的污水量均为12000吨,由于污水厂处于调试阶段,污水处理能力有限,该企业投资自建设备处理污水,两种处理方式同时进行.1至6月,该企业向污水厂输送的污水量y1(吨)与月份x(1≤x≤6,且x取整数)之间满足的函数关系如下表:
月份x(月) | 1 | 2 | 3 | 4 | 5 | 6 |
输送的污水量y1(吨) | 12000 | 6000 | 4000 | 3000 | 2400 | 2000 |
7至12月,该企业自身处理的污水量y2(吨)与月份x(7≤x≤12,且x取整数)之间满足二次函数关系式为y2=ax2+c(a≠0).其图象如图所示.1至6月,污水厂处理每吨污水的费用:z1(元)与月份x之间满足函数关系式:z1=![]() x,该企业自身处理每吨污水的费用:z2(元)与月份x之间满足函数关系式:z2=
x,该企业自身处理每吨污水的费用:z2(元)与月份x之间满足函数关系式:z2=![]() x﹣
x﹣![]() x2;7至12月,污水厂处理每吨污水的费用均为2元,该企业自身处理每吨污水的费用均为1.5元.
x2;7至12月,污水厂处理每吨污水的费用均为2元,该企业自身处理每吨污水的费用均为1.5元.
(1)请观察题中的表格和图象,用所学过的一次函数、反比例函数或二次函数的有关知识,分别直接写出y1,y2与x之间的函数关系式;
(2)请你求出该企业去年哪个月用于污水处理的费用W(元)最多,并求出这个最多费用.