题目内容
【题目】“如果二次函数
的图象与
轴有两个公共点,那么一元二次方程
有两个不相等的实数根.”请根据你对这句话的理解,解决下面问题:若
、
（＜）是关于的方程
的两根且
＜
则请用“＜”来表示、、、的大小是_________.
【答案】p＜a＜b＜q.
【解析】
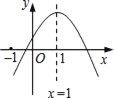
依题意画出函数y=（x﹣a）（x﹣b）图象草图，根据二次函数的增减性求解．
依题意，画出函数y=（x﹣a）（x﹣b）的图象，如图所示．
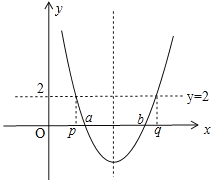
函数图象为抛物线，开口向上，与x轴两个交点的横坐标分别为a，b（a＜b）．
方程2﹣（x﹣a）（x﹣b）=0
转化为（x﹣a）（x﹣b）=2，方程的两根是抛物线y=（x﹣a）（x﹣b）与直线y=2的两个交点．
由p＜q，可知对称轴左侧交点横坐标为p，右侧为q．
由抛物线开口向上，则在对称轴左侧，y随x增大而减少，则有p＜a；在对称轴右侧，y随x增大而增大，则有b＜q．
综上所述：可知p＜a＜b＜q．
故答案为：p＜a＜b＜q．
练习册系列答案
阅读快车系列答案
相关题目
【题目】在日历上，我们可以发现其中某些数满足一定的规律，如图是2012年8月份的日历. 我们任意选择其中所示的方框部分，将每个方框部分中4个位置上的数交叉相乘，再相减，例如：
，
，不难发现，结果都是7.
（1）请你再选择两个类似的部分试一试，看看是否符合这个规律；
（2）请你利用整式的运算对以上的规律加以证明.
日 | 一 | 二 | 三 | 四 | 五 | 六 |
1 | 2 | 3 | 4 | |||
5 | 6 | 7 | 8 | 9 | 10 | 11 |
12 | 13 | 14 | 15 | 16 | 17 | 18 |
19 | 20 | 21 | 22 | 23 | 24 | 25 |
26 | 27 | 28 | 29 | 30 | 31 |
