Question

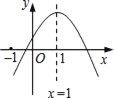
【题目】如图是抛物线y=ax2+bx+c（a≠0）图象的一部分，抛物线的顶点坐标A（1，3），与x轴的一个交点B（4，0），有下列结论：①2a+b=0，②abc＞0；③方程ax2+bx+c=3有两个相等的实数根，④当y＜0时，﹣2＜x＜4，其中正确的是（　　）

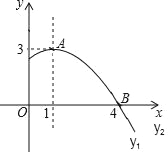
A. ②③ B. ①③ C. ①③④ D. ①②③④

Answer 1

【答案】B

【解析】

根据二次函数的性质、方程与二次函数的关系、函数与不等式的关系一一判断即可．

①∵抛物线的对称轴x=﹣=1，

∴b=﹣2a，即2a+b=0，故此结论正确；

②∵由图可知a＜0、c＞0，

∴b=﹣2a＞0，

则abc＜0，故此结论错误；

③由图象可知该抛物线与直线y=3只有唯一交点A（1，3），

∴方程ax2+bx+c=3有两个相等的实数根，此结论正确；

④抛物线与x轴的交点为（4，0）且抛物线的对称轴为x=1，

则抛物线与x轴的另一交点为（﹣2，0），

∴当y＜0时，x＜﹣2或x＞4，此结论错误；

综上所述：①③正确，

故选：B．