Question

【题目】△ABC中，∠ABC＝30°，AB＝4，AC＝4，则BC＝____．

Answer 1

【答案】8或4．

【解析】

分两种情况进行解答，一是∠ACB为锐角，另一种∠ACB为钝角，分别画出图形，通过作高，构造直角三角形，利用直角三角形的性质和边角关系进行解答即可．

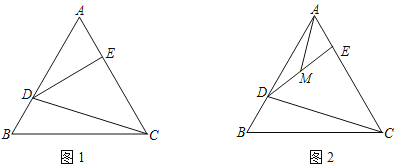
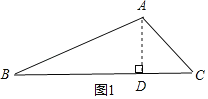
①当∠ACB为锐角时，如图1，过点A作AD⊥BC，垂足为D，

在Rt△ABD中，∵∠ABC＝30°，AB＝4，

∴AD＝AB＝2，BD＝cos30°×AB＝6，

在Rt△ADC中，DC＝＝2，

∴BC＝AD+DC＝6+2＝8；

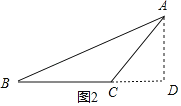
②当∠ACB为钝角时，如图2，过点A作AD⊥BC，交BC的延长线于点D，

在Rt△ABD中，∵∠ABC＝30°，AB＝4，

∴AD＝AB＝2，BD＝cos30°×AB＝6，

在Rt△ADC中，DC＝＝2，

∴BC＝AD﹣DC＝6﹣2＝4；

因此BC的长为8或4，

故答案为：8或4．