题目内容
【题目】某林业部门要考察某种幼树在一定条件下的移植成活率，在同样的条件下对这种幼树进行大量移植，并统计成活情况，记录如下（其中频率结果保留小数点后三位）
移植总数（n） | 10 | 50 | 270 | 400 | 750 | 1500 | 3500 | 7000 | 9000 |
成活数（m） | 8 | 47 | 235 | 369 | 662 | 1335 | 3203 | 6335 | 8118 |
成活的频率 | 0.800 | 0.940 | 0.870 | 0.923 | 0.883 | 0.890 | 0.915 | 0.905 | 0.902 |
由此可以估计幼树移植成活的概率为 ．
【答案】0.892
【解析】解： 
=（0.800+0.940+0.870+0.923+0.883+0.890+0.915+0.905+0.902）÷9=0.892，∴这种幼树移植成活率的概率约为0.892．
故本题答案为：0.892．
【考点精析】根据题目的已知条件，利用用频率估计概率的相关知识可以得到问题的答案，需要掌握在同样条件下，做大量的重复试验，利用一个随机事件发生的频率逐渐稳定到某个常数，可以估计这个事件发生的概率．
练习册系列答案
名校课堂系列答案
相关题目
【题目】某校为了增强学生体质，推动“阳光体育”运动的广泛开展，学校准备购买一批运动鞋供学生借用，学校体育部从八年级随机抽取了部分学生的鞋号，绘制了如下的统计图①和②，请根据相关信息，解答下列问题：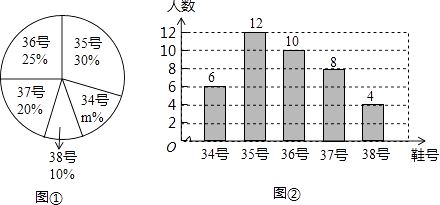 
（1）图①中m的值为；
（2）本次调查获取的样本数据的众数是 ， 中位数是；
（3）该校计划购买200双运动鞋，校体育部对各种鞋号运动鞋的购买数量做出如下估计：
根据样本数据分析得知：各种鞋号的运动鞋购买数量如下： |
请你分析：校体育部的估计是否合理？如果合理，请将体育部的估算过程补充完整，若不合理，请说明理由，并且给学校提一个合理化的建议．
