Question

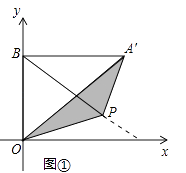
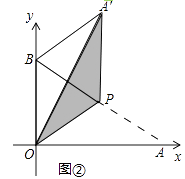
【题目】如图，坐标平面上，△ABC与△DEF全等，其中A、B、C的对应顶点分别为D、E、F，且AB=BC=5．若A点的坐标为（﹣3，1），B、C两点在直线y=﹣3上，D、E两点在y轴上．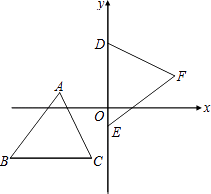
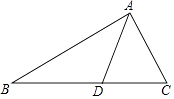
（1）在△ABC中，作AH、CK分别垂直BC、AB于H、K，求证：KC=HA；
（2）求F点到y轴的距离．

Answer 1

【答案】
（1）证明：如图，AH⊥BC于H，CK⊥AB于K．

∴∠DPF=∠AKC=∠CHA=90°，

∵AB=BC，

∴∠BAC=∠BCA，

在△AKC和△CHA中，

，

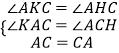∴△AKC≌△CHA，

∴KC=HA

（2）作PF⊥DE于E．

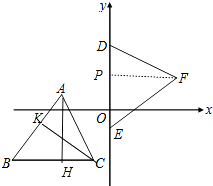
∵B、C在y=﹣3上，且点A的坐标为（﹣3，1），

∴AH=4，

∴KC=AH=4，

∵△ABC≌△DEF，

∴∠BAC=∠EDF，AC=DF，

在△AKC和△DPF中，

，

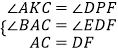∴△AKC≌△DPF，

∴KC=PF=4．

∴F点到y轴的距离4．

【解析】（1）欲证明KC=HA，只要证明△AKC≌△CHA即可．（2）作PF⊥DE于E，只要证明△AKC≌△DPF即可．