Question

【题目】如图，一艘海轮位于小岛C的南偏东60°方向，距离小岛120海里的A处，该海轮从A处正北方向航行一段距离后，到达位于小岛C北偏东45°方向的B处．

（1）求该海轮从A处到B处的航行过程中与小岛C之间的最短距离（记过保留根号）；
（2）如果该海轮以每小时20海里的速度从B处沿BC方向行驶，求它从B处到达小岛C的航行时间（结果精确到0.1小时）．（参考数据： =1.41， =1.73）

Answer 1

【答案】
（1）

解：如图，过点C作CD⊥AB于D，

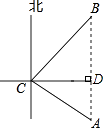
由题意，得∠ACD=30°．

在直角△ACD中，∠ADC=90°，

∴cos∠ACD= ，

∴CD=ACcos30°=120× =60 （海里）；

（2）

解：在直角△BCD中，∠BDC=90°，∠DCA=45°，

∴cos∠BCD= ，

∴BC= = =60 ≈60×2.44=146.4（海里），

∴146.4÷20=7.32≈7.3（小时）．

【解析】答：（1）求该海轮从A处到B处的航行过程中与小岛C之间的最短距离是60 海里；（2）如果该海轮以每小时20海里的速度从B处沿BC方向行驶，求它从B处到达小岛C的航行时间约为7.3小时．
（1）首先过点C作CD⊥AB于D，构建直角△ACD，通过解该直角三角形得到CD的长度即可；（2）通过解直角△BCD来求BC的长度．
【考点精析】掌握关于方向角问题是解答本题的根本，需要知道指北或指南方向线与目标方向 线所成的小于90°的水平角，叫做方向角．