Question

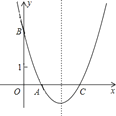
【题目】如图，已知抛物线 与 轴交于A、C两点，与 轴交于点B，在抛物线的对称轴上找一点Q，使△ABQ成为等腰三角形，则Q点的坐标是____.

Answer 1

【答案】Q1，Q2，Q3（2，2），Q4（2，3）

【解析】

先求得点A和点B的坐标，由顶点式知抛物线的对称轴为直线x=2，设抛物线的对称轴上的点Q的坐标为，分别求得，并用含的代数式表示的长，分三种情况构造方程求得的值.

如图，

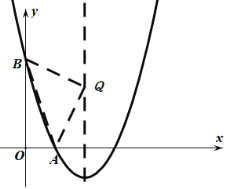
抛物线的对称轴为直线x=2

当y=0时，

（x-2）2-1=0

解之：x1=3，x2=1

∴点A的坐标为（1，0）

当x=0时，y=3

∴点B（0，3）

设点Q的坐标为（2，m）.

∴AB2=32+1=10，BQ2=（m-3）2+22=（m-3）2+4，AQ2=m2+1，

要使△ABQ为等腰三角形，

当AB2=BQ2时，则（m-3）2+4=10,

解之：m1= ， m2= ，

∴点Q1 ， Q2.

当BQ2=AQ2时，则（m-3）2+4=m2+1,

解之：m=2

所以点Q2（2，2）；

当AB2=AQ2时，则10=m2+1,

解之：m=±3

若m=-3，则点B、A，Q在同一直线上，

∴m=-3舍去，

∴点Q4（2，3）

故答案为：，Q2，（2，2），（2，3）