Question

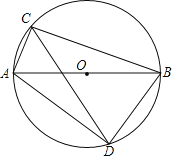
【题目】如图，AB是⊙O的直径，点C，D分别在两个半圆上（不与点A、B重合），AD、BD的长分别是方程x2﹣2x+（m2﹣2m+13）＝0的两个实数根．

（1）若∠ADC＝15°，求CD的长；

（2）求证：AC+BC＝CD．

Answer 1

【答案】（1）；（2）见解析

【解析】

（1）根据AD、BD的长分别是方程x2﹣2x+（m2﹣2m+13）＝0的两个实数根，可以求得AD、BD的长，从而可以求得∠DBA和∠DAB的度数，由∠ADC=15°，可以求得∠ABC的度数，作辅助线DE⊥CD于点E，从而可以求得CD的长；（2）作辅助线DE⊥BC于点E，DF⊥CA交CA的延长线于点F，画出相应的图形，然后进行灵活变化，即可证明所要证明的结论．

解：（1）∵AD、BD的长分别是方程x2﹣2x+（m2﹣2m+13）＝0的两个实数根，

∴△＝，

又∵

∴m﹣1＝0，得m＝1，

∴ ，

解得，，

即AD＝BD＝，

∵AB是⊙O的直径，点C，D分别在两个半圆上（不与点A、B重合），

∴∠ADB＝90°，

∴∠DAB＝∠DBA＝45°，

作DE⊥BC于点E，如下图一所示，

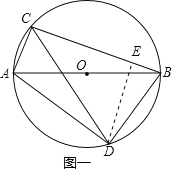
∵∠ADC＝15°，∠ADB＝90°，

∴∠ABC＝∠ADC＝15°，∠CDB＝75°，

∴∠DBE＝∠DBA+∠ABC＝60°，

∴∠DCE＝180°﹣∠CDB﹣∠DBE＝45°，

∵BD=，

∴DE＝BDsin60°＝，

∵∠DEC＝90°，DE＝，∠DCE＝45°，

∴CD＝；

（2）证明：作DE⊥BC于点E，DF⊥CA交CA的延长线于点F，如下图二所示，

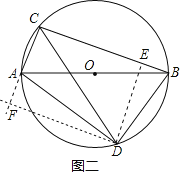
由（1）可得，DE＝EC，

∵∠DEC＝∠ECA＝∠CFD＝90°，

∴四边形CFDE是正方形，

∴DF＝CE，

∵∠AFD＝∠BFD＝90°，DA＝DB，

∴在Rt△AFD和Rt△BED中

∴Rt△AFD≌Rt△BED（HL），

∴BE＝AF，

∴BC+AC＝BE+CE+AC＝AF+AC+CE＝CF+CE＝2CE，

∵，

∴BC+AC＝2CE＝＝，

即AC+BC＝CD．