题目内容
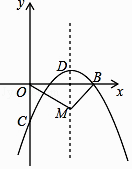
【题目】如图,在矩形![]() 中,
中,![]() ,点
,点![]() 从点
从点![]() 出发,沿
出发,沿![]() 向点
向点![]() 匀速运动,速度为每秒1个单位,过点
匀速运动,速度为每秒1个单位,过点![]() 作
作![]() ,交对角线
,交对角线![]() 于点
于点![]() .点
.点![]() 从点
从点![]() 出发,沿对角线
出发,沿对角线![]() 向点
向点![]() 匀速运动,速度为每秒1个单位.
匀速运动,速度为每秒1个单位. ![]() 、
、![]() 两点同时出发,设它们的运动时间为
两点同时出发,设它们的运动时间为![]() 秒(
秒(![]() ).
).
(1)当![]() 时,求出
时,求出![]() 的值;
的值;
(2)连接![]() ,当
,当![]() 时,求出
时,求出![]() 的值;
的值;
(3)试探究:当![]() 为何值时,
为何值时,![]() 是等腰三角形?
是等腰三角形?


【答案】(1)t=![]() ;(2)t=
;(2)t=![]() ;(3)满足条件的时间t为
;(3)满足条件的时间t为![]() 或
或![]() 或
或![]() 或
或![]() .
.
【解析】(1)判断出△PBQ∽△DBC得出比例式建立方程即可得出结论;
(2)先判断出△BPM∽△BCD得出比例式求出PM=6-![]() t,BM=10-
t,BM=10-![]() t,再判断出△ADM∽△PBQ,得出比例式建立方程即可得出结论;
t,再判断出△ADM∽△PBQ,得出比例式建立方程即可得出结论;
(3)分两种情况利用等腰三角形的性质即可得出结论.
(1)在矩形ABCD中,AB=CD=6,BC=8,∴∠C=90°,BD=10,
根据题意得,CP=BQ=t,BP=8﹣t,∵PQ⊥BD,∴∠BQP=90°,∴∠BQP=∠C,
∵∠PBQ=∠DBC=45°,∴△PBQ∽△DBC,∴![]() ,∴
,∴![]() ,∴t=
,∴t=![]() ;
;
(2)∵PM⊥BC,∠C=90°,∴PM∥CD,∴△BPM∽△BCD,∴![]() ,
,
∴![]() ,∴PM=6﹣
,∴PM=6﹣![]() t,BM=10﹣
t,BM=10﹣![]() t,∴DM=
t,∴DM=![]() t,
t,
∵PQ∥AM,∴∠AMQ=∠MQP,∴∠AMD=∠PQB,
∵四边形ABCD是矩形,∴AD∥BC,∴∠ADM=∠PBQ,∴△ADM∽△PBQ,
∴![]() ,∴
,∴ ,∴t=
,∴t=![]() ;
;
(3)

①当点Q在线段BM上时,
Ⅰ、若PM=MQ,∴6﹣![]() t=10﹣
t=10﹣![]() t,∴t=
t,∴t=![]() ,
,
Ⅱ、若PM=PQ时,如图1,作PN⊥MQ于N,
∴∠PNM=90°,MN=![]() MQ=
MQ=![]() (10﹣
(10﹣![]() t)=5﹣
t)=5﹣![]() t,∴∠PNM=∠C,
t,∴∠PNM=∠C,
∵PM∥CD,∴∠PMQ=∠BDC,∴△PMN∽△BDC,
∴![]() ,∴
,∴ ,∴t=
,∴t=![]() ,
,
Ⅲ、若MQ=PQ时,如备用图1,作QE⊥PM于E,∴QE∥BP,ME=![]() PM,
PM,
∴△QEM∽△BPM,∴![]() ,∴MQ=BQ,∴10﹣
,∴MQ=BQ,∴10﹣![]() t=t,∴t=
t=t,∴t=![]() ,
,
②当点M在线段BQ上时,如备用图2,∠PMQ是钝角,∴只可能PM=QM,
∴6﹣![]() t=t﹣(10﹣
t=t﹣(10﹣![]() t),∴t=
t),∴t=![]() ,即:满足条件的时间t为
,即:满足条件的时间t为![]() 或
或![]() 或
或![]() 或
或![]() .
.

 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案