题目内容
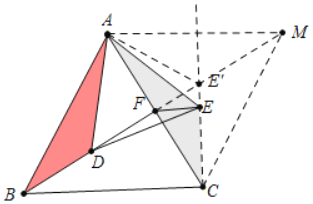
【题目】如图，等边△ABC中，BF是AC边上中线，点D在BF上，连接AD，在AD的右侧作等边△ADE，连接EF，当△AEF周长最小时，∠CFE的大小是（ ）
A. 30° B. 45° C. 60° D. 90°
【答案】D
【解析】分析：首先证明点E在射线CE上运动（∠ACE=30°），
因为AF为定值，所以当AE+EF最小时，△AEF的周长最小，
作点A关于直线CE的对称点M，连接FM交CE 于E′，此时AE′+FE′的值最小，
根据等边三角形的判定和性质即可求出∠CFE的大小．
详解：∵△ABC，△ADE都是等边三角形，
∴AB=AC，AD=AE，∠BAC=∠DAE=∠ABC=60°，
∴∠BAD=∠CAE，
∴△BAD≌△CAE，
∴∠ABD=∠ACE，
∵AF=CF，
∴∠ABD=∠CBD=∠ACE=30°，
∴点E在射线CE上运动（∠ACE=30°），
作点A关于直线CE的对称点M，连接FM交CE 于E′，此时AE′+FE′的值最小，
∵CA=CM，∠ACM=60°，
∴△ACM是等边三角形，
∵AF=CF，
∴FM⊥AC，
∴∠CFE′=90°，
故选：D．
练习册系列答案
阅读快车系列答案
相关题目
