Question

【题目】如图，在中，是边上的中线，是中点，过点作，交的延长线于点交于点，连接交于点.

(1)判断四边形的形状，并说明理由;

(2)若，且，求四边形的面积.

(3)连接，求证：.

Answer 1

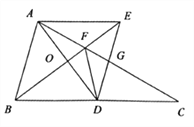
【答案】（1）四边形ABDE是菱形．理由见解析；（2）12；（3）见解析.

【解析】（1）先判定△AOE≌△DOB（ASA），得出AE=BD，根据AE∥BD，即可得出四边形ABDE是平行四边形，再根据BD=BA，即可得到平行四边形ABDE是菱形；
（2）根据四边形ABDE是菱形，AB=，且OA：OB=2：3，运用勾股定理求得AD=4，BE=6，即可得出菱形ABDE的面积；
（3）根据菱形的性质得出∠GDF=∠DCF，再根据∠GFD=∠DFC，即可判定△DFG∽△CFD，进而得到，据此可得DF2=FGFC．

（1）四边形ABDE是菱形．理由如下：

∵AE∥BC，∴∠EAO=∠BDO，∵O是AD中点，∴AO=DO，

在△AOE和△DOB中，，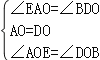

∴△AOE≌△DOB（ASA），∴AE=BD，

又∵AE∥BD，∴四边形ABDE是平行四边形，

∵AD是BC边上的中线，∴BC=2BD，

又∵BC=2AB，∴BD=BA，∴平行四边形ABDE是菱形；

（2）∵四边形ABDE是菱形，∴AD⊥BE，AO=AD，BO=BE，

设OA=2k，OB=3k，在Rt△AOB中，由勾股定理得，4k2+9k2=13，解得k=1，

∴OA=2，OB=3，∴AD=4，BE=6，

∴菱形ABDE的面积=×4×6=12；

（3）证明：∵四边形ABDE是菱形，

∴BE垂直平分AD，∴EA=ED，FA=FD，

∴∠EAO=∠EDO，∠FAO=∠FDO，∴∠EAF=∠EDF，

∵AE∥BC，∴∠EAO=∠DCF，∴∠GDF=∠DCF，

又∵∠GFD=∠DFC，

∴△DFG∽△CFD，

∴=，∴DF2=FGFC．