题目内容
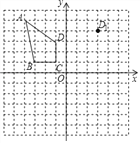
【题目】如图,在平面直角坐标系中,已知抛物线y=ax2+bx﹣2(a≠0)与x轴交于A(1,0)、B(3,0)两点,与y轴交于点C,其顶点为D. 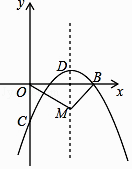
(1)求抛物线的解析式;
(2)一动点M从点D出发,以每秒1个单位的速度沿抛物线的对称轴向下运动,连OM,BM,设运动时间为t秒(t=0),在点M的运动过程中,当∠OMB=90°时,求t的值.
【答案】
(1)解:∵抛物线y=ax2+bx﹣2(a≠0)与x轴交于A(1,0)、B(3,0)两点,
∴ ![]() ,
,
解得: 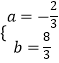 ,
,
∴抛物线的解析式为:y=﹣ ![]() x2+
x2+ ![]() x﹣2
x﹣2
(2)解:∵y=﹣ ![]() x2+
x2+ ![]() x﹣2=﹣
x﹣2=﹣ ![]() (x﹣2)2+
(x﹣2)2+ ![]() ,
,
∴D(2, ![]() ),
),
设M(2,m),
∵O( 0,0),B(3,0),
∵∠OMB=90°,
∴OM2+BM2=OB2,
即m2+22+(3﹣2)2+m2=9,
∴m= ![]() ,
,
∵ ![]() >
> ![]() ,
,
∴M(2,﹣ ![]() ),
),
∴DM= ![]() +
+ ![]() ,
,
∴t= ![]() +
+ ![]()
【解析】(1)把A(1,0)、B(3,0)代入y=ax2+bx﹣2,即可得到结果;(2)由y= ![]() x2+
x2+ ![]() x﹣2=
x﹣2= ![]() (x﹣2)2+
(x﹣2)2+ ![]() ,得到D(2,
,得到D(2, ![]() ),设M(2,m),根据勾股定理列方程得到M(2,﹣
),设M(2,m),根据勾股定理列方程得到M(2,﹣ ![]() ),于是得到结论.
),于是得到结论.
【考点精析】关于本题考查的抛物线与坐标轴的交点,需要了解一元二次方程的解是其对应的二次函数的图像与x轴的交点坐标.因此一元二次方程中的b2-4ac,在二次函数中表示图像与x轴是否有交点.当b2-4ac>0时,图像与x轴有两个交点;当b2-4ac=0时,图像与x轴有一个交点;当b2-4ac<0时,图像与x轴没有交点.才能得出正确答案.

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案
相关题目