题目内容
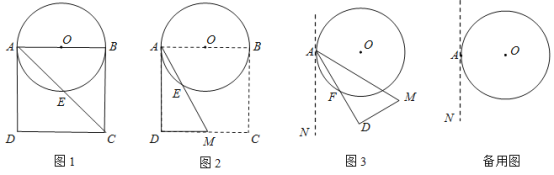
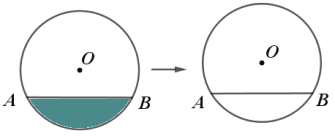
【题目】如图,![]() 是一个圆柱体污水管道的横截面,管道中有部分污水,污水液面横截面宽度(即
是一个圆柱体污水管道的横截面,管道中有部分污水,污水液面横截面宽度(即![]() 长)为
长)为![]() 污水管道直径为
污水管道直径为![]() 则弦
则弦![]() 所对圆周角的大小为_____________________
所对圆周角的大小为_____________________![]()
【答案】![]() 或
或![]()
【解析】
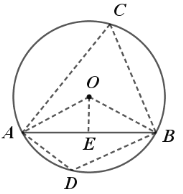
过点O作OE⊥AB于点E,在弦AB所对的劣弧上取一个点D,在弦AB所对的优弧上取一个点C,根据圆周角定理以及垂径定理可求出结果.
如图,过点O作OE⊥AB于点E,在弦AB所对的劣弧上取一个点D,在弦AB所对的优弧上取一个点C,
由题意得:AB=![]() ,OA=1,
,OA=1,
,∵OE⊥AB,
∵AE=![]() AB=
AB=![]() ,
,
在Rt△AEO中,∵sin∠AOE=![]() =
=![]() ,
,
∴∠AOE=60°,
同理可得:∠BOE=60°
∴∠AOB=120°
∴∠ACB=![]() ∠AOB=
∠AOB=![]() ×120°=60°
×120°=60°
∵四边形ADBC是圆内接四边形,
∴∠ADB+∠ACB=180°,
∴∠ADB=180°-∠ACB=180°-60°=120°,
故弦AB所对圆周角的大小为60°或120°,
故填:60或120.

【题目】甲、乙两种水稻实验品种连续5年的平均单位面积产量如下(单位:吨/公顷):
品种 | 2015年 | 2016年 | 2017年 | 2018年 | 2019年 |
甲 |
|
|
| 10 |
|
乙 |
|
|
|
|
|
(1)乙种水稻5年的平均单位面积产量的平均数为______吨/公顷;
(2)“扇形统计图”和“折线统计图”中,更能直观地反映甲种水稻5年的平均单位面积产量变化过程和趋势的统计图是______;
(3)王老汉家有100公顷田要种植水稻,你建议他种什么品种的水稻,并说明理由.
【题目】红树林学校在七年级新生中举行了全员参加的“防溺水”安全知识竞赛,试卷题目共10题,每题10分.现分别从三个班中各随机取10名同学的成绩(单位:分),收集数据如下:
1班:90,70,80,80,80,80,80,90,80,100;
2班:70,80,80,80,60,90,90,90,100,90;
3班:90,60,70,80,80,80,80,90,100,100.
整理数据:
分数 人数 班级 | 60 | 70 | 80 | 90 | 100 |
1班 | 0 | 1 | 6 | 2 | 1 |
2班 | 1 | 1 | 3 |
| 1 |
3班 | 1 | 1 | 4 | 2 | 2 |
分析数据:
平均数 | 中位数 | 众数 | |
1班 | 83 | 80 | 80 |
2班 | 83 |
|
|
3班 |
| 80 | 80 |
根据以上信息回答下列问题:
(1)请直接写出表格中![]() 的值;
的值;
(2)比较这三组样本数据的平均数、中位数和众数,你认为哪个班的成绩比较好?请说明理由;
(3)为了让学生重视安全知识的学习,学校将给竞赛成绩满分的同学颁发奖状,该校七年级新生共570人,试估计需要准备多少张奖状?
【题目】港珠澳大桥(英文名称:Hong Kong-Zhuhai-Macao Bridge)是中国境内一座连接香港、广东珠海和澳门的桥隧工程,位于中国广东省珠江口伶洋海域内,为珠江三角洲地区环线高速公路南环段.港珠澳大桥于![]() 年
年![]() 月
月![]() 日动工建设;于
日动工建设;于![]() 年
年![]() 月
月![]() 日实现主体工程全线贯通;于
日实现主体工程全线贯通;于![]() 年
年![]() 月
月![]() 日完成主体工程验收;同年
日完成主体工程验收;同年![]() 月
月![]() 日上午
日上午![]() 时开通运营.广东某校数学“综合与实践”小组的同学把“测量港珠澳大桥某一段斜拉索顶端到桥面的距离”作为一项课题活动,他们制订了测量方案,并利用课余时间完成该桥斜拉索实地测量,测量结果如下表
时开通运营.广东某校数学“综合与实践”小组的同学把“测量港珠澳大桥某一段斜拉索顶端到桥面的距离”作为一项课题活动,他们制订了测量方案,并利用课余时间完成该桥斜拉索实地测量,测量结果如下表
项目 | 内容 | ||
课题 | 测量港珠澳大桥某一段斜拉索顶端到桥面的距离 | ||
测量示意图 |
| 说明:两侧斜拉索 | |
测量数据 |
|
|
|
|
|
| |
|
| ||

(1)请帮助该小组根据上表中的测量数据,求斜拉索顶端点![]() 到
到![]() 的距离(参考数据:
的距离(参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() );
);
(2)该小组要写出一份完整的课题活动报告,除上表的项目外,你认为还需要补充哪些项目(写出一个即可)?