题目内容
【题目】复课返校后,为了拉大学生锻炼的间距,某学校决定增购适合独立训练的两种体育器材:跳绳和毽子.已知跳绳的单价比毽子的单价多![]() 元,用
元,用![]() 元购买的跳绳个数和用
元购买的跳绳个数和用![]() 元购买的子数量相同.
元购买的子数量相同.
(1)求跳绳和毯子的单价分别是多少元?
(2)学校计划购买跳绳和毯子两种器材共![]() 个,由于受疫情影响,商场决定对这两种器材打折销售,其中跳绳以八折出售,毽子以七五折出售,学校要求跳绳的数量不少于毽子数量的
个,由于受疫情影响,商场决定对这两种器材打折销售,其中跳绳以八折出售,毽子以七五折出售,学校要求跳绳的数量不少于毽子数量的![]() 倍,跳绳的数量不多于
倍,跳绳的数量不多于![]() 根,请你求出学校花钱最少的购买方案.
根,请你求出学校花钱最少的购买方案.
【答案】(1)跳绳的售价为![]() 元,毯子的售价为
元,毯子的售价为![]() 元;(2)学校花钱最少的购买方案为:购进跳绳
元;(2)学校花钱最少的购买方案为:购进跳绳![]() 根,毯子
根,毯子![]() 个.
个.
【解析】
(1)设毽子的单价为x元,则跳绳的单价为(x+4)元,根据数量=总价÷单价结合用1000元购买的跳绳个数和用800元购买的键子数量相同,即可得出关于x的分式方程,解之经检验后即可得出结论;
(2)设购买毽子m个,则购买跳绳(400-m)根,根据跳绳的数量不少于毽子数量的3倍且跳绳的数量不多于310根,即可得出关于m的一元一次不等式组,解之即可得出m的取值范围,设学校购买跳绳和毽子两种器材共花w元,根据总价=单价×数量可得出w关于m的函数关系式,再利用一次函数的性质即可解决最值问题.
(1)设毯子的售价为![]() 元,则跳绳的售价为
元,则跳绳的售价为![]() 元
元
依题意得:![]()
解得:![]()
经检验,![]() 是分式方程的解
是分式方程的解
![]() (元)
(元)
答:跳绳的售价为![]() 元,毯子的售价为
元,毯子的售价为![]() 元
元
(2)设购买毽子m个,则购买跳绳(400-m)根,
依题意,得:![]() ,
,
解得:90≤m≤100.
设学校购买跳绳和毽子两种器材共花w元,则w=20×0.8(400-m)+16×0.75m=-4m+6400.
∵-4<0,
∴w随m的增大而减小,
∴当m=100时,w取得最小值,最小值=-4×100+6400=6000.
答:当学校购买300根跳绳、100个毽子时,总费用最少.

 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
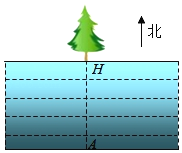
小学教材完全解读系列答案【题目】为了测量一条两岸平行的河流宽度,三个数学研究小组设计了不同的方案,他们在河南岸的点A处测得河北岸的树H恰好在A的正北方向.测量方案与数据如下表:
课题 | 测量河流宽度 | ||
测量工具 | 测量角度的仪器,皮尺等 | ||
测量小组 | 第一小组 | 第二小组 | 第三小组 |
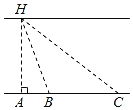
测量方案示意图 |
|
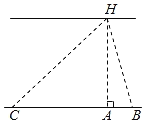
|
|
说明 | 点B,C在点A的正东方向 | 点B,D在点A的正东方向 | 点B在点A的正东方向,点C在点A的正西方向. |
测量数据 | BC=60m, ∠ABH=70°, ∠ACH=35°. | BD=20m, ∠ABH=70°, ∠BCD=35°. | BC=101m, ∠ABH=70°, ∠ACH=35°. |
(1)哪个小组的数据无法计算出河宽?
(2)请选择其中一个方案及其数据求出河宽(精确到0.1m).(参考数据:sin70°≈0.94,sin35°≈0.57,tan70°≈2.75,tan35°≈0.70)
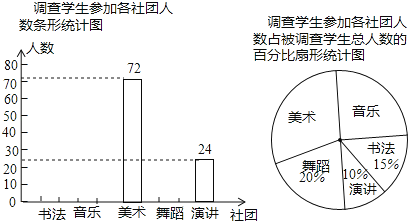
【题目】车间有20名工人,某天他们生产的零件个数统计如下表.
车间20名工人某一天生产的零件个数统计表
生产零件的个数(个) | 9 | 10 | 11 | 12 | 13 | 15 | 16 | 19 | 20 |
工人人数(人) | 1 | 1 | 6 | 4 | 2 | 2 | 2 | 1 | 1 |
(1)求这一天20名工人生产零件的平均个数;
(2)为了提高大多数工人的积极性,管理者准备实行“每天定额生产,超产有奖”的措施.如果你是管理者,从平均数、中位数、众数的角度进行分析,你将如何确定这个“定额”?