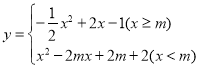题目内容
【题目】一个不透明的口袋中有![]() 个大小、质地完全相同的乒乓球,球面上分别标有数-1,2,-3,4.
个大小、质地完全相同的乒乓球,球面上分别标有数-1,2,-3,4.
(1)摇匀后任意摸出![]() 个球,则摸出的乒乓球球面上的数是正数的概率为 _;
个球,则摸出的乒乓球球面上的数是正数的概率为 _;
(2)掘匀后先从中任意摸出![]() 个球(不放回),记下数字作为平面直角坐标系内点
个球(不放回),记下数字作为平面直角坐标系内点![]() 的横坐标:再从余下的
的横坐标:再从余下的![]() 个球中任意摸出
个球中任意摸出![]() 个球,记下数字作为点
个球,记下数字作为点![]() 的纵坐标,用列表或画树状图的方法求:两次摸球后得到的点
的纵坐标,用列表或画树状图的方法求:两次摸球后得到的点![]() 恰好在函数
恰好在函数![]() 图像上的概率.
图像上的概率.
【答案】(1)![]() ;(2)两次摸球后得到的点
;(2)两次摸球后得到的点![]() 恰好在函数
恰好在函数![]() 图像的概率为
图像的概率为![]()
【解析】
(1)直接利用概率公式计算;
(2)利用列表法,展示所有12种等可能的结果数,找出两次摸球后得到的点![]() 恰好在函数
恰好在函数![]() 图像上的结果数,然后根据公式求解.
图像上的结果数,然后根据公式求解.
解:(1)摸出的乒乓球球面上的数是正数的概率为:![]() ;
;
故答案为:![]() ;
;
![]() 用列表法表示为:
用列表法表示为:
点
|
|
|
|
|
|
|
|
| |
|
|
|
| |
|
|
|
| |
|
|
|
|
∴共有![]() 种等可能的结果,其中两次摸球后得到的点
种等可能的结果,其中两次摸球后得到的点![]() 恰好在函数
恰好在函数![]() 图像的有
图像的有![]() 种,
种,
设事件“两次摸球后得到的点![]() 恰好在函数
恰好在函数![]() ”,
”,
则![]() ;
;
答:两次摸球后得到的点![]() 恰好在函数
恰好在函数![]() 图像的概率为
图像的概率为![]() ;
;

练习册系列答案
 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案 小学期末标准试卷系列答案
小学期末标准试卷系列答案
相关题目