题目内容
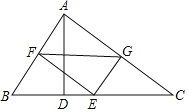
【题目】如图,在△ABC中,∠BAC=90°,AD是BC边上的高,E是BC边上的一个动点(不与B,C重合),EF⊥AB,EG⊥AC,垂足分别为F,G.
(1)求证:![]() ;
;
(2)FD与DG是否垂直?若垂直,请给出证明;若不垂直,请说明理由;
(3)当![]() 的值为多少时,△FDG为等腰直角三角形?
的值为多少时,△FDG为等腰直角三角形?
【答案】(1)见解析;(2)FD与DG垂直,理由见解析;(3)当![]() 时,△FDG为等腰直角三角形,理由见解析.
时,△FDG为等腰直角三角形,理由见解析.
【解析】
(1)由比例线段可知,我们需要证明△ADC∽△EGC,由两个角对应相等即可证得;
(2)由矩形的判定定理可知,四边形AFEG为矩形,根据矩形的性质及相似三角形的判定可得到△AFD∽△CGD,从而不难得到结论;
(3)先判断出DF=DG,再利用同角的余角相等判断出∠ADF=∠CDG,∠BAD=∠C,得出△ADF≌△CDG,即可得出结论.
(1)证明:在△ADC和△EGC中,
∵∠ADC=∠EGC,∠C=∠C,
∴△ADC∽△EGC.
∴![]() .
.
(2)解:FD与DG垂直.
理由如下:
在四边形AFEG中,
∵∠FAG=∠AFE=∠AGE=90°,
∴四边形AFEG为矩形.
∴AF=EG.
∵![]() ,
,
∴![]() .
.
又∵△ABC为直角三角形,AD⊥BC,
∴∠FAD=∠C=90°﹣∠DAC,
∴△AFD∽△CGD.
∴∠ADF=∠CDG.
∵∠CDG+∠ADG=90°,
∴∠ADF+∠ADG=90°.
即∠FDG=90°.
∴FD⊥DG.

(3)解:当![]() 的值为1时,△FDG为等腰直角三角形,理由如下:
的值为1时,△FDG为等腰直角三角形,理由如下:
由(2)知,∠FDG=90°,
∵△DFG为等腰直角三角形,
∴DF=DG,
∵AD是BC边上的高,
∴∠ADC=90°,
∴∠ADG+∠CDG=90°,
∵∠FDG=90°,
∴∠ADG+∠ADF=90°,
∴∠ADF=∠CDG,
∵∠CAD+∠BAD=90°,∠C+∠CAD=90°,
∴∠BAD=∠C,
∴△ADF≌△CDG(AAS),
∴AD=CD,
∵∠ADC=90°,
∴∠C=45°=∠B,
∴AB=AC,
即:当![]() 的值为1时,△FDG为等腰直角三角形.
的值为1时,△FDG为等腰直角三角形.