题目内容
【题目】某商场购进一种每件价格为90元的新商品,在商场试销时发现:销售单价![]() 元
元![]() 件
件![]() 与每天销售量
与每天销售量![]() 件
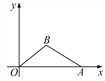
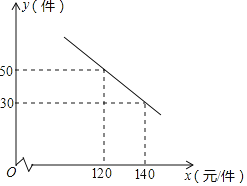
件![]() 之间满足如图所示的关系.
之间满足如图所示的关系.
![]() 求出y与x之间的函数关系式;
求出y与x之间的函数关系式;
![]() 写出每天的利润W与销售单价x之间的函数关系式,并求出售价定为多少时,每天获得的利润最大?最大利润是多少?
写出每天的利润W与销售单价x之间的函数关系式,并求出售价定为多少时,每天获得的利润最大?最大利润是多少?
【答案】(1)y=-x+170;(2)W=﹣x2+260x﹣1530,售价定为130元时,每天获得的利润最大,最大利润是1600元.
【解析】
(1)先利用待定系数法求一次函数解析式;
(2)用每件的利润乘以销售量得到每天的利润W,即W=(x﹣90)(﹣x+170),然后根据二次函数的性质解决问题.
(1)设y与x之间的函数关系式为y=kx+b,根据题意得:![]() ,解得:
,解得:![]() ,∴y与x之间的函数关系式为y=﹣x+170;
,∴y与x之间的函数关系式为y=﹣x+170;
(2)W=(x﹣90)(﹣x+170)=﹣x2+260x﹣15300.
∵W=﹣x2+260x﹣15300=﹣(x﹣130)2+1600,而a=﹣1<0,∴当x=130时,W有最大值1600.
答:售价定为130元时,每天获得的利润最大,最大利润是1600元.

练习册系列答案
 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目