Question

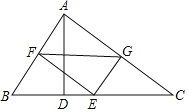
【题目】如图，菱形ABCD边长为6，∠BAD＝120°，点E、F分别在AB、AD上且BE＝AF，则EF的最小值为_____，

Answer 1

【答案】3

【解析】

连接AC，根据菱形的性质得到∠B＝60°，AB＝BC，推出△ABC是等边三角形，得到AC＝BC，∠B＝∠CAF＝60°，根据全等三角形的性质得到CE＝CF，∠BCE＝∠ACF，求得△CEF是等边三角形，得到EF＝CE，于是得到当CE⊥AB时，CE最小，即EF最小，解直角三角形即可得到结论．

解：连接AC，

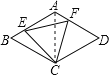
∵四边形ABCD是菱形，∠BAD＝120°，

∴∠B＝60°，AB＝BC，

∴△ABC是等边三角形，

∴AC＝BC，∠B＝∠CAF＝60°，

∵BE＝AF，

∴△BCE≌△ACF（SAS），

∴CE＝CF，∠BCE＝∠ACF，

∴∠ECF＝∠ACB＝60°，

∴△CEF是等边三角形，

∴EF＝CE，

∴当CE⊥AB时，CE最小，即EF最小，

∵CE⊥AB，

∴∠CEB＝90°，

∵∠B＝60°，

∴CE＝BC＝3，

∴EF的最小值为3，

故答案为：3．