题目内容
【题目】在平面直角坐标系中,点A、B、C坐标分别为(0,1)、(0,5)、(3,0),D是平面内一点,且∠ADB=45°,则线段CD的最大值是__________
【答案】![]()
【解析】
根据D是平面内一点,且∠ADB=45°,可以构建圆心为P的圆,判断出C,P,D在一条直线上为最大值,根据已知条件求出P的坐标,进而求出半径及PC得值,从而得到答案.
解:如图 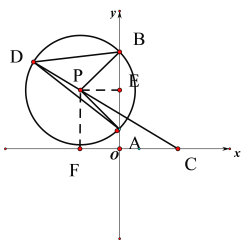
设圆心为点P,连接PA,PB,PC,最大值为C,P,D在一条直线上
∵ 点A、B、C坐标分别为(0,1)、(0,5)、(3,0),D是平面内一点,且∠ADB=45°
∴ ∠APB=90°则PE=2,圆的半径=![]()
∴ P(-2,3) PE=FO=2,PF=EO=3,PD=![]()
∴ PC2=PF2+CF2=OE2+(PE+OC)2=32+(2+3)2=34
∴ PC=![]()
∴ 线段CD的最大值:CD=PC+PD=![]()
故此题为:![]()

练习册系列答案
相关题目