Question

【题目】将两条邻边长分别为，1的矩形纸片剪成四个等腰三角形纸片（无余纸片），各种剪法剪出的等腰三角形中，其中一个等腰三角形的腰长可以是下列数中的_____（填序号）．

①，②1，③﹣1，④，⑤．

Answer 1

【答案】①②③④．

【解析】

首先作出图形，再根据矩形的性质和等腰三角形的判定即可求解．

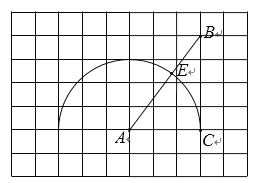
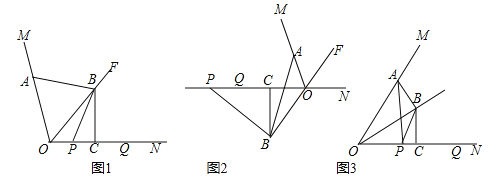
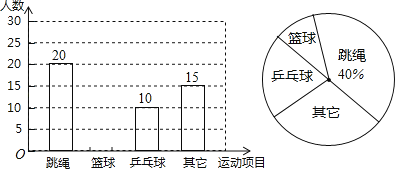
解：如下图所示：在BC上截取BE=1，连接AE

∴△ABE为等腰直角三角形，AB=BE=1，AE=，CE=BC－BE=

∴∠BAE=45°，∠EAD=90°－∠BAE=45°

在AE上截取AF=1，连接DF、CF

∴EF=AE－AF==CE

∴△EFC为等腰三角形，腰长为

过点F作FG⊥AD于G

∴AG=AF·cos∠FAG=

∴DG=AD－AG=

∴FG垂直平分AD

∴AF=FD=1

∴△AFD为等腰三角形，腰长为1

△DFC为等腰三角形，腰长为1；

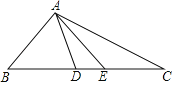
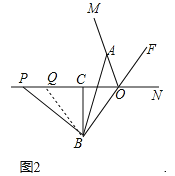
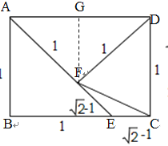
如下图所示：在AD上截取DF=1，连接BF

∴△DFC为等腰直角三角形，腰长为1，AF=AD－DF=

根据勾股定理可得CF=

∴△CBF为等腰三角形，腰长为

在AB上截取AE==AF

∴△AEF为等腰直角三角形，腰长为，BE=AB－AE=

根据勾股定理可得EF==BE

∴△EBF为等腰三角形，腰长为；

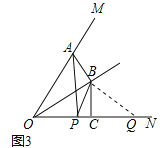
如下图所示：连接AC、BD交于点E

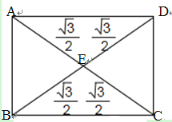
易知△EAB、△EBC、△ECD和△EAD均为等腰三角形

利用勾股定理AC=

∴AE=BE=CE=DE=．

综上：其中一个等腰三角形的腰长可以是①，②1，③﹣1，④，不可以是．

故答案为：①②③④．