Ő‚ńŅńŕ»›
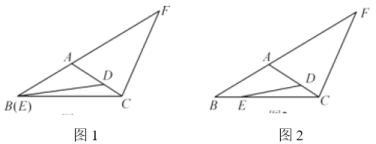
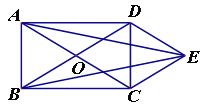
°ĺŐ‚ńŅ°Ņő Ő‚£ļ»ÁÕľ£¨‘ŕ°ųABD÷–£¨BA£ĹBD£ģ‘ŕBDĶń—”≥§ŌŖ…Ō»°Ķ„E£¨C£¨◊ų°ųAEC£¨ ĻEA£ĹEC£¨»Ű°ŌBAE£Ĺ90°„£¨°ŌB£Ĺ45°„£¨«ů°ŌDACĶń∂» ż£ģ
īūįł£ļ°ŌDAC£Ĺ45°„
ňľŅľ£ļ£®1£©»ÁĻŻį—“‘…Ō°įő Ő‚°Ī÷–ĶńŐűľĢ°į°ŌB£Ĺ45°„°Ī»•ĶŰ£¨∆š”ŗŐűľĢ≤ĽĪš£¨ń«√ī°ŌDACĶń∂» żĽŠłńĪš¬ū£ŅňĶ√ųņŪ”…£Ľ
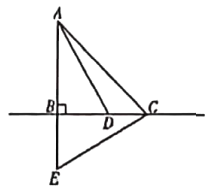
£®2£©»ÁĻŻį—“‘…Ō°įő Ő‚°Ī÷–ĶńŐűľĢ°į°ŌB£Ĺ45°„°Ī»•ĶŰ£¨‘ŔĹę°į°ŌBAE£Ĺ90°„°Īłńő™°į°ŌBAE£Ĺn°„°Ī£¨∆š”ŗŐűľĢ≤ĽĪš£¨«ů°ŌDACĶń∂» ż£ģ
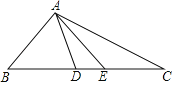
°ĺīūįł°Ņ£®1£©°ŌDACĶń∂» ż≤ĽĽŠłńĪš£¨÷Ķő™45°„£Ľ£®2£©![]() n°„£ģ
n°„£ģ
°ĺĹ‚őŲ°Ņ
£®1£©łýĺ›Ķ»—Ł»żĹ«–őĶń–‘÷ Ķ√ĶĹ°ŌAED£Ĺ2°ŌC£¨ĘŔ«ůĶ√°ŌDAE£Ĺ90°„-°ŌBAD£Ĺ90°„-£®45°„+°ŌC£©£Ĺ45°„©Ā°ŌC£¨Ęŕ”…ĘŔ£¨ĘŕľīŅ…Ķ√ĶĹĹŠ¬Ř£Ľ
£®2£©…Ť°ŌABC£Ĺm°„£¨łýĺ›»żĹ«–őĶńńŕĹ«ļÕ∂®ņŪļÕĶ»—Ł»żĹ«–őĶń–‘÷ ľīŅ…Ķ√ĶĹĹŠ¬Ř£ģ
Ĺ‚£ļ£®1£©°ŌDACĶń∂» ż≤ĽĽŠłńĪš£Ľ
°ŖEA£ĹEC£¨
°ŗ°ŌAED£Ĺ2°ŌC£¨ĘŔ
°Ŗ°ŌBAE£Ĺ90°„£¨
°ŗ°ŌBAD£Ĺ![]() [180°„©Ā£®90°„©Ā2°ŌC£©]£Ĺ45°„+°ŌC£¨
[180°„©Ā£®90°„©Ā2°ŌC£©]£Ĺ45°„+°ŌC£¨
°ŗ°ŌDAE£Ĺ90°„©Ā°ŌBAD£Ĺ90°„©Ā£®45°„+°ŌC£©£Ĺ45°„©Ā°ŌC£¨Ęŕ
”…ĘŔ£¨ĘŕĶ√£¨°ŌDAC£Ĺ°ŌDAE+°ŌCAE£Ĺ45°„£Ľ
£®2£©…Ť°ŌABC£Ĺm°„£¨
‘Ú°ŌBAD£Ĺ![]() £®180°„©Ām°„£©£Ĺ90°„©Ā
£®180°„©Ām°„£©£Ĺ90°„©Ā![]() m°„£¨°ŌAEB£Ĺ180°„©Ān°„©Ām°„£¨
m°„£¨°ŌAEB£Ĺ180°„©Ān°„©Ām°„£¨
°ŗ°ŌDAE£Ĺn°„©Ā°ŌBAD£Ĺn°„©Ā90°„+![]() m°„£¨
m°„£¨
°ŖEA£ĹEC£¨
°ŗ°ŌCAE£Ĺ![]() °ŌAEB£Ĺ90°„©Ā
°ŌAEB£Ĺ90°„©Ā![]() n°„©Ā
n°„©Ā![]() m°„£¨
m°„£¨
°ŗ°ŌDAC£Ĺ°ŌDAE+°ŌCAE£Ĺn°„©Ā90°„+![]() m°„+90°„©Ā
m°„+90°„©Ā![]() n°„©Ā
n°„©Ā![]() m°„£Ĺ
m°„£Ĺ![]() n°„£ģ
n°„£ģ