Question

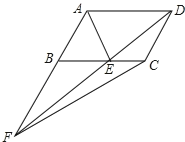
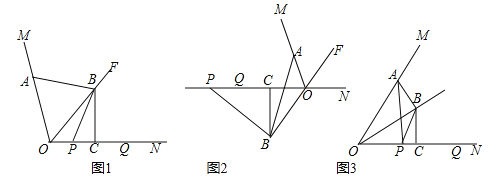
【题目】如图，OF是∠MON的平分线，点A在射线OM上，P，Q是直线ON上的两动点，点Q在点P的右侧，且PQ=OA，作线段OQ的垂直平分线，分别交直线OF、ON交于点B、点C，连接AB、PB．

（1）如图1，当P、Q两点都在射线ON上时，请直接写出线段AB与PB的数量关系；

（2）如图2，当P、Q两点都在射线ON的反向延长线上时，线段AB，PB是否还存在（1）中的数量关系？若存在，请写出证明过程；若不存在，请说明理由；

（3）如图3，∠MON=60°，连接AP，设=k，当P和Q两点都在射线ON上移动时，k是否存在最小值？若存在，请直接写出k的最小值；若不存在，请说明理由．

【答案】（1）AB=PB；（2）存在；（3）k=0.5．

【解析】试题分析：（1）结论：AB=PB．连接BQ，只要证明△AOB≌△PQB即可解决问题；

（2）存在．证明方法类似（1）；

（3）连接BQ．只要证明△ABP∽△OBQ，即可推出=，由∠AOB=30°，推出当BA⊥OM时， 的值最小，最小值为0.5，由此即可解决问题；

试题解析：解：（1）连接：AB=PB．理由：如图1中，连接BQ．

∵BC垂直平分OQ，∴BO=BQ，∴∠BOQ=∠BQO，∵OF平分∠MON，∴∠AOB=∠BQO，∵OA=PQ，∴△AOB≌△PQB，∴AB=PB．

（2）存在，理由：如图2中，连接BQ．

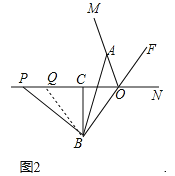
∵BC垂直平分OQ，∴BO=BQ，∴∠BOQ=∠BQO，∵OF平分∠MON，∠BOQ=∠FON，∴∠AOF=∠FON=∠BQC，∴∠BQP=∠AOB，∵OA=PQ，∴△AOB≌△PQB，∴AB=PB．

（3）连接BQ．

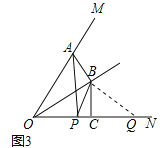
易证△ABO≌△PBQ，∴∠OAB=∠BPQ，AB=PB，∵∠OPB+∠BPQ=180°，∴∠OAB+∠OPB=180°，∠AOP+∠ABP=180°，∵∠MON=60°，∴∠ABP=120°，∵BA=BP，∴∠BAP=∠BPA=30°，∵BO=BQ，∴∠BOQ=∠BQO=30°，∴△ABP∽△OBQ，∴ =，∵∠AOB=30°，∴当BA⊥OM时， 的值最小，最小值为0.5，∴k=0.5．

点睛：本题考查相似综合题、全等三角形的判定和性质、相似三角形的判定和性质等知识，解题的关键是正确寻找全等三角形解决问题，学会用转化的思想思考问题，属于中考常考题型．

【题型】解答题
【结束】
28

【题目】如图，已知抛物线y=ax2+x+c与x轴交于A，B两点，与y轴交于丁C，且A（2，0），C（0，﹣4），直线l：y=﹣x﹣4与x轴交于点D，点P是抛物线y=ax2+x+c上的一动点，过点P作PE⊥x轴，垂足为E，交直线l于点F．

（1）试求该抛物线表达式；

（2）如图（1），若点P在第三象限，四边形PCOF是平行四边形，求P点的坐标；

（3）如图（2），过点P作PH⊥y轴，垂足为H，连接AC．

①求证：△ACD是直角三角形；

②试问当P点横坐标为何值时，使得以点P、C、H为顶点的三角形与△ACD相似？

Answer 1

【答案】（1）y=x2+x﹣4；（2）点P的坐标为（﹣，﹣）或（﹣8，﹣4）；（3）点P的横坐标为﹣5.5或﹣10.5或2或﹣18时，使得以点P、C、H为顶点的三角形与△ACD相似．

【解析】试题分析：（1）利用待定系数法列方程求解析式.(2)把P，F点坐标用m表示写出来，利用四边形PCOF是平行四边形得到m值，求得P点坐标.(3) ①由两点间的距离公式可知分别计算AC，CD，AD勾股定理逆定理知三角形是直角三角形；②分类讨论，△ACD∽△CHP，△ACD∽△PHC分别计算P点坐标.

试题解析：

解：（1）由题意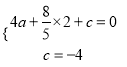得： ，解得： ，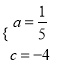

∴抛物线的表达式为y=x2+x﹣4．

（2）设P（m， m2+m﹣4），则F（m，﹣m﹣4）．

∴PF=（﹣m﹣4）﹣（m2+m﹣4）=﹣m2﹣m．

∵PE⊥x轴，

∴PF∥OC．

∴PF=OC时，四边形PCOF是平行四边形．

∴﹣m2﹣m=4，解得：m=﹣或m=﹣8．

当m=﹣时， m2+m﹣4=﹣，

当m=﹣8时， m2+m﹣4=﹣4．

∴点P的坐标为（﹣，﹣）或（﹣8，﹣4）．

（3）①证明：把y=0代入y=﹣x﹣4得：﹣x﹣4=0，解得：x=﹣8．

∴D（﹣8，0）．

∴OD=8．

∵A（2，0），C（0，﹣4），

∴AD=2﹣（﹣8）=10．

由两点间的距离公式可知：AC2=22+42=20，DC2=82+42=80，AD2=100，

∴AC2+CD2=AD2．

∴△ACD是直角三角形，且∠ACD=90°．

②由①得∠ACD=90°．

当△ACD∽△CHP时， ，即，

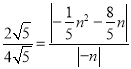解得：n=0（舍去）或n=﹣5.5或n=﹣10.5．

当△ACD∽△PHC时， ，即，

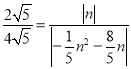解得：n=0（舍去）或n=2或n=﹣18．

综上所述，点P的横坐标为﹣5.5或﹣10.5或2或﹣18时，使得以点P、C、H为顶点的三角形与△ACD相似．