题目内容
【题目】如图,矩形ABCD的顶点A、B的坐标分别为(-4,0)和(2,0),BC=![]() .设直线AC与直线x=4交于点E.
.设直线AC与直线x=4交于点E.
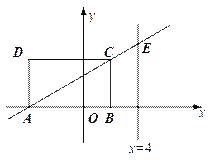
(1)求以直线x=4为对称轴,且过C与原点O的抛物线的函数关系式,并说明此抛物线一定过点E;
(2)设(1)中的抛物线与x轴的另一个交点为N,M是该抛物线上位于C、N之间的一动点,求△CMN面积的最大值.
【答案】(1)略
(2)![]()
【解析】
解:(1)点C的坐标![]() .设抛物线的函数关系式为y=a(x–4)2+m,
.设抛物线的函数关系式为y=a(x–4)2+m,
则![]() ,解得
,解得![]()
∴所求抛物线的函数关系式为![]() …………①
…………①
设直线AC的函数关系式为![]() 则
则![]() ,解得
,解得![]() .
.
∴直线AC的函数关系式为![]() ,∴点E的坐标为
,∴点E的坐标为![]()
把x=4代入①式,得![]() ,∴此抛物线过E点.
,∴此抛物线过E点.
(2)(1)中抛物线与x轴的另一个交点为N(8,0),设M(x,y),
过M作MG⊥x轴于G,
则S△CMN=S△MNG+S梯形MGBC—S△CBN=![]()
=![]()
=![]()
∴当x=5时,S△CMN有最大值![]()

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目