题目内容
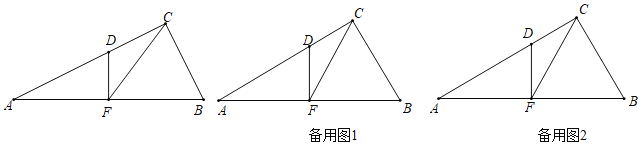
【题目】如图,△ABC是等边三角形,AC上有一点D,分别以BD为边作等边△BDE和等腰△BDF,边BC、DE交于点H,点F在BA延长线上且DB=DF,连接CE.
(1)若AB=8,AD=4,求△BDF的面积;
(2)求证:BC=AF+CE.

【答案】(1)12![]() ;(2)详见解析.
;(2)详见解析.
【解析】
(1)作DH⊥AB于H,如图1,利用等边三角形的性质得点D为AC的中点,则BD⊥AD,利用含30度的直角三角形三边的关系计算出DH、BF,从而得到△BDF的面积;
(2)如图2,先证明△BAD≌△BCE得到AD=CE,∠4=∠3=60°,再证明∠ADF=∠HBD=∠5,则可判断△ADF≌△CED,从而得到AF=CD,所以AC=AD+CD=CE+AF=BC.
(1)解:作DH⊥AB于H,如图1,
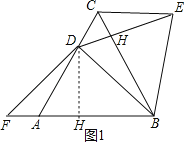
∵△ABC是等边三角形,AB=8,AD=4,
∴点D为AC的中点,∠CAB=60°
∴BD⊥AD,
∴∠ADB=90°,
∵DH⊥AB,
∴FH=BH,∠ADH=30°
在Rt△ADH中,AH=![]() AD=2,
AD=2,
∴BH=6,DH=![]() =2
=2![]() ,
,
∴BH=HF=6,
∴△BDF的面积=![]() ×(6+6)×2
×(6+6)×2![]() =12
=12![]() ;
;
(2)证明:如图2,
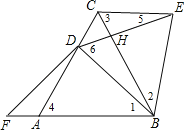
∵△ABC、△DEB都为等边三角形,
∴∠4=∠ABC=∠DBE=∠6=60°,BA=BC,BD=BE
∴∠1=∠2,
在△BAD和△BCE中
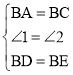 ,
,
∴△BAD≌△BCE(SAS),
∴AD=CE,∠4=∠3=60°,
而∠CHE=∠DHB,
∴∠5=∠HBD,
∵∠4=∠F+∠ADF=60°,∠HBD+∠1=60°,
而∠1=∠F,
∴∠ADF=∠HBD=∠5,
在△ADF和△CED中
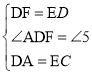
∴△ADF≌△CED(SAS),
∴AF=CD,
∴AC=AD+CD=CE+AF,
∴BC=AF+CE.

练习册系列答案
 新思维寒假作业系列答案
新思维寒假作业系列答案
相关题目