题目内容
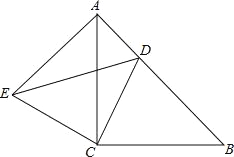
【题目】如图,在△ABC中,∠ACB=90°,AC=15,BC=9,点P是线段AC上的一个动点,连接BP,将线段BP绕点P逆时针旋转90°得到线段PD,连接AD,则线段AD的最小值是______.

【答案】3![]()
【解析】
如图,过点D作DE⊥AC于E,有旋转的性质可得DP=BP,∠DPB=90°,由“AAS”可证△DEP≌△PCB,可得DE=CP,EP=BC=9,可求AE+DE=6,由勾股定理和二次函数的性质可求解.
如图,过点D作DE⊥AC于E,
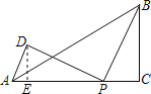
∵将线段BP绕点P逆时针旋转90°得到线段PD,
∴DP=BP,∠DPB=90°,
∴∠DPE+∠BPC=90°,且∠BPC+∠PBC=90°,
∴∠DPE=∠PBC,且DP=BP,∠DEP=∠C=90°,
∴△DEP≌△PCB(AAS)
∴DE=CP,EP=BC=9,
∵AE+PC=AC-EP=6
∴AE+DE=6,
∵AD2=AE2+DE2,
∴AD2=AE2+(6-AE)2,
∴AD2=2(AE-3)2+18,
当AE=3时,AD有最小值为3![]() ,
,
故答案为3![]() .
.

练习册系列答案
相关题目