��Ŀ����
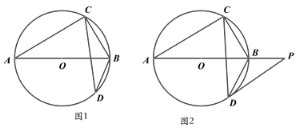
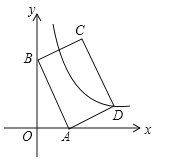
����Ŀ����֪����ͼ����ƽ��ֱ������ϵ�У���![]() Ϊ����ԭ�㣬
Ϊ����ԭ�㣬![]() ��ֱ��
��ֱ��![]() ��
��![]() �ύ�ڵ�A����
�ύ�ڵ�A����![]() ���ڵ�B����C����ֱ��AB�Ĵ��ߣ�����ΪE����
���ڵ�B����C����ֱ��AB�Ĵ��ߣ�����ΪE����![]() ���ڵ�D��
���ڵ�D��
��1����ֱ��CD�Ľ���ʽ��
��2����GΪ![]() �Ḻ������һ�㣬����EG������E��
�Ḻ������һ�㣬����EG������E��![]() ��
��![]() ���ڵ�H�����G������Ϊ
���ڵ�H�����G������Ϊ![]() ���߶�AH�ij�Ϊ
���߶�AH�ij�Ϊ![]() ����
����![]() ��
��![]() ֮��ĺ�����ϵʽ����Ҫ��д���Ա�����ȡֵ��Χ��
֮��ĺ�����ϵʽ����Ҫ��д���Ա�����ȡֵ��Χ��
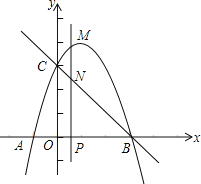
��3������C��![]() ��Ĵ��ߣ�����G��
��Ĵ��ߣ�����G��![]() ��Ĵ��ߣ����߽��ڵ�M������H��
��Ĵ��ߣ����߽��ڵ�M������H��![]() �ڵ�N����ֱ��CD�ڵ�
�ڵ�N����ֱ��CD�ڵ�![]() ������MK����MKƽ��
������MK����MKƽ��![]() ����
����![]() ��ֵ��
��ֵ��
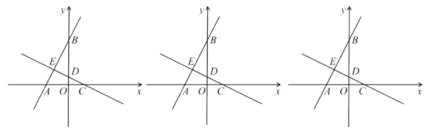
���𰸡���1��![]() ����2��
����2��![]() ����3��
����3��![]()
��������
��1�����ݻ��ഹֱ��ֱ��б�ʻ�Ϊ-1�����ֱ��CE�Ľ���ʽ���ٽ���C������뼴����⣻
��2������E��![]() ��y���ڵ�M������E��
��y���ڵ�M������E��![]() ���ڵ�N��ͨ����ֱ�������ο�֤
���ڵ�N��ͨ����ֱ�������ο�֤![]() ��
��![]() ��
��![]() ��
��![]() ���õ�AN=DM��HN=GM�������õ�
���õ�AN=DM��HN=GM�������õ�![]() ���ٸ���CE����ʽ���D�����꣬�����ҳ�
���ٸ���CE����ʽ���D�����꣬�����ҳ�![]() ��
��![]() ֮��ĺ�����ϵʽ��
֮��ĺ�����ϵʽ��
��3������B��![]() �ڵ�T����ֱ��BT�Ͻ�ȡ
�ڵ�T����ֱ��BT�Ͻ�ȡ![]() ��֤�ı���
��֤�ı���![]() ���ı���
���ı���![]() ��Ϊ���Σ���
��Ϊ���Σ���![]() ���ٽ�һ��֤��
���ٽ�һ��֤��![]() ��
��![]() ������ȫ�������ε�����ͨ���Ƕȼ��㣬�ó���BMLΪ������������
������ȫ�������ε�����ͨ���Ƕȼ��㣬�ó���BMLΪ������������![]() �����ú���t�Ĵ���ʽ��ʾBM�������Rt��BMG�����ù��ɶ���������ʽ�����t��ֵ��
�����ú���t�Ĵ���ʽ��ʾBM�������Rt��BMG�����ù��ɶ���������ʽ�����t��ֵ��
�⣺��1����CE��AB��
����ֱ��CE�Ľ���ʽΪ��![]() ��
��
�ѵ�![]() ��2��0��������������ʽ����
��2��0��������������ʽ����![]() ��
��
��ֱ��CD�Ľ���ʽΪ��![]() ��
��
��2������E��![]() ��y���ڵ�M������E��
��y���ڵ�M������E��![]() ���ڵ�N��
���ڵ�N��
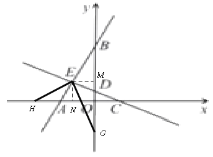
��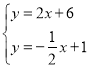 ��
��
���![]() ��
��
��![]() ��
��
��֤![]() ��
��![]() ��
��![]() ��
��![]() ��
��
��AN=DM��HN=GM��
��![]() ��
��
��ֱ��CE�Ľ���ʽ![]() �������D��0��1��
�������D��0��1��
��DG=1��t��
��![]() ��
��
��3������B��![]() �ڵ�T����ֱ��BT�Ͻ�ȡ
�ڵ�T����ֱ��BT�Ͻ�ȡ![]() ��
��
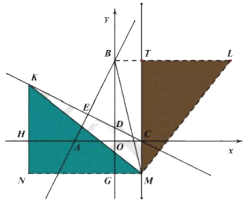
��֤�ı���![]() ���ı���
���ı���![]() ��Ϊ���Σ�
������
�ɣ�2���ʿ�֪![]() ����
����![]()
��![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ��
��![]() ��
��
��![]() ��
��
��![]() ����
����![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ��
�У�
![]() ��
��
���![]() ������������ȥ����
������������ȥ����![]()
�ʣ�![]() ��
��

 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�