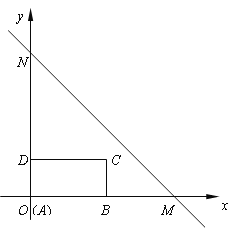
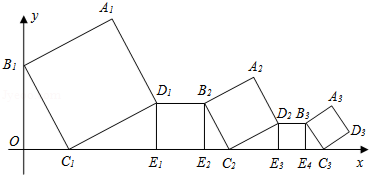
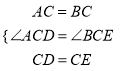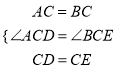题目内容
【题目】解不等式组: ![]() .请结合题意填空,完成本体的解法.
.请结合题意填空,完成本体的解法.
![]()
(1)解不等式(1),得________;
(2)解不等式(2),得________;
(3)把不等式 (1)和 (2)的解集在数轴上表示出来.
(4)原不等式的解集为________.
【答案】(1)x<5;(2)x≥2;(3)见解析;(4)2≤x<5
【解析】试题分析:(1)先去括号,再移项,合并同类项,把x的系数化为1即可;
(2)先移项,合并同类项,把x的系数化为1即可;
(3)把两个不等式的解集在数轴上表示出来即可;
(4)写出两个不等式的公共解集即可.
试题解析:解:(1)去括号得,5>3x﹣12+2,移项得,5+12﹣2>3x,合并同类项得,15>3x,把x的系数化为1得,x<5.
故答案为:x<5;
(2)移项得,2x≥1+3,合并同类项得,2x≥4,x的系数化为1得,x≥2.
故答案为:x≥2;
(3)把不等式 (1)和 (2)的解集在数轴上表示为:
![]() ;
;
(4)由(3)得,原不等式的解集为:2≤x<5.
故答案为:2≤x<5.

练习册系列答案
 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目