题目内容
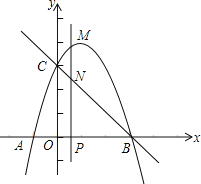
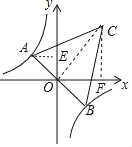
【题目】如图,在反比例函数y=-![]() 的图象上有一动点A,连结AO并延长交图象的另一支于点B,在第一象限内有一点C,满足AC=BC,当点A运动时,点C始终在函数y=
的图象上有一动点A,连结AO并延长交图象的另一支于点B,在第一象限内有一点C,满足AC=BC,当点A运动时,点C始终在函数y=![]() 的图象上运动,若tan∠CAB=3,则k的值为( )
的图象上运动,若tan∠CAB=3,则k的值为( )
A.![]() B.6C.8D.18
B.6C.8D.18
【答案】D
【解析】
连接OC,过点A作AE⊥y轴于点E,过点C作CF⊥x轴于点F,通过角的计算找出∠AOE=∠COF,结合“∠AEO=90°,∠CFO=90°”可得出△AOE∽△COF,根据相似三角形的性质得出![]() ,再由tan∠CAB=
,再由tan∠CAB=![]() =3,可得出CFOF=18,由此即可得出结论.
=3,可得出CFOF=18,由此即可得出结论.
解:连接OC,过点A作AE⊥y轴于点E,过点C作CF⊥x轴于点F,如图所示.
由直线AB与反比例函数![]() 的对称性可知A、B点关于O点对称,
的对称性可知A、B点关于O点对称,
∴AO=BO.
又∵AC=BC,
∴CO⊥AB.
∵∠AOE+∠EOC=90°,∠EOC+∠COF=90°,
∴∠AOE=∠COF,
又∵∠AEO=90°,∠CFO=90°,
∴△AOE∽△COF,
∴![]()
∵tan∠CAB=![]() =3,
=3,
∴CF=3AE,OF=3OE.
又∵AEOE=|﹣2|=2,CFOF=|k|,
∴k=±18.
∵点C在第一象限,
∴k=18.
故选D.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目