Question

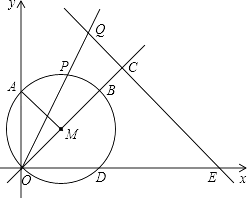
【题目】如图，在平面直角坐标系中，OA=OB，点P为△ABO的角平分线的交点，若PN⊥PA交x轴于N，延长OP交AB于M，写出AO，ON，PM之间的数量关系，并证明之．

Answer 1

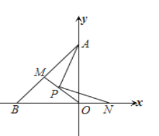
【答案】AO-ON=2PM，证明见解析

【解析】

作 PE⊥x轴于E，PF⊥y轴于F，求出PF=PE，∠APF=∠NPE，根据ASA证△APF≌△NPE，推出AF=EN即可．

AO-ON=2PM，证明如下：

作 PE⊥x轴于E，PF⊥y轴于 F，则∠AFP=∠NEP=90°，

∵P是△AOB角平分线交点，∴PF=PE

∵PE⊥x轴，PF⊥y轴

∴∠PFO=∠PEO=∠FOE=90°，∴∠FPE=90°

∵AP⊥PN，

∴∠APN=90°=∠FPE

∴∠APN-∠FPN=∠FPE-∠FPN

即∠APF=∠NPE

在与中

∴

∴

∴AO-ON =（AF+OF）-（NE-OE）=2OE=2PF=2PM

即AO-ON=2PM．