题目内容
【题目】已知二次函数y=x2+bx+c，其图象抛物线交x轴于点A（1，0），B（3，0），交y轴于点C，直线l过点C，且交抛物线于另一点E（点E不与点A、B重合）．
（1）求此二次函数关系式；
（2）若直线l1经过抛物线顶点D，交x轴于点F，且l1∥l，则以点C、D、E、F为顶点的四边形能否为平行四边形？若能，求出点E的坐标；若不能，请说明理由．
（3）若过点A作AG⊥x轴，交直线l于点G，连接OG、BE，试证明OG∥BE．
【答案】
（1）
解：二次函数y=x2+bx+c，其图象抛物线交x轴于点A（1，0），B（3，0），
∴ 
，
解得： 
，
∴此二次函数关系式为：y=x2﹣4x+3；
（2）
解：假设以点C、D、E、F为顶点的四边形能成为平行四边形．
①若CD为平行四边形的对角线，如答图2﹣1．
过点D作DM⊥AB于点M，过点E作EN⊥OC于点N，
∵y=x2﹣4x+3=（x﹣2）2﹣1，
∴点D（2，﹣1），点C（0，3），
∴DM=1，
∵l1∥l，
∴当CE=DF时，四边形CEDF是平行四边形，
∴∠ECF+∠CFD=180°，
∵∠OCF+∠OFC=90°，
∴∠ECN+∠DFM=90°，
∵∠DFM+∠FDM=90°，
∴∠ECN=∠FDM，
在△ECN和△FDM中，
，
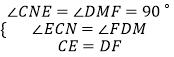∴△ECN≌△FDM（AAS），
∴CN=DM=1，
∴ON=OC﹣CN=3﹣1=2，
当y=2时，x2﹣4x+3=2，
解得：x=2± 
；
当x=2± 时，可得E（2+ ，2），F（﹣ ，0）或E（2﹣ ，2，），F（ ，0），
此时四边形CFDE为平行四边形．
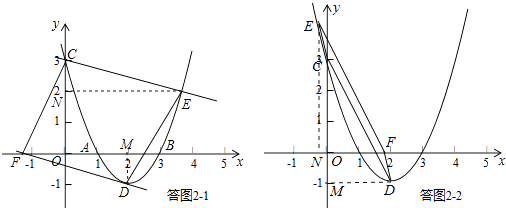
②若CD为平行四边形的边，如答图2﹣2，则EF∥CD，且EF=CD．
过点D作DM⊥y轴于点M，则DM=2，OM=1，CM=OM+OC=4；
过点E作EN⊥x轴于点N．
易证△CDM≌△EFN，∴EN=CM=4．
∴x2﹣4x+3=4，
解得：x=2± 
．
综上所述，以点C、D、E、F为顶点的四边形能成为平行四边形；点E的坐标为（2+ ，2）、（2﹣ ，2）、（2+ ，4）、（2﹣ ，4）．
（3）
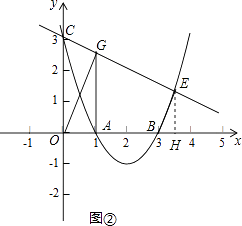
解：如图②，过点E作EH⊥x轴于点H，
设直线CE的解析式为：y=kx+3，
∵A（1，0），AG⊥x轴，
∴点G（1，k+3），
即OA=1，AG=k+3，
∵E是直线与抛物线的交点，
∴ 
，
解得： 
，
∴点E（k+4，（k+1）（k+3）），
∴BH=OH﹣OB=k+1，EH=（k+1）（k+3），
∴ 
，
∵∠OAG=∠BHE=90°，
∴△OAG∽△BHE，
∴∠AOG=∠HBE，
∴OG∥BE．
【解析】（1）由二次函数y=x2+bx+c，其图象抛物线交x轴于点A（1，0），B（3，0），直接利用待定系数法求解，即可求得此二次函数关系式；（2）以点C、D、E、F为顶点的四边形构成平行四边形，有两种情形，需要分类讨论，避免漏解：①若CD为平行四边形的对角线，如答图2﹣1所示；②若CD为平行四边形的边，如答图2﹣2所示；（3）首先过点E作EH⊥x轴于点H，设直线CE的解析式为：y=kx+3，然后分别求得点G与E的坐标，即可证得△OAG∽△BHE，则可得∠AOG=∠HBE，继而可证得OG∥BE．
【考点精析】关于本题考查的二次函数的图象和二次函数的性质，需要了解二次函数图像关键点：1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点；增减性：当a>0时，对称轴左边，y随x增大而减小；对称轴右边，y随x增大而增大；当a<0时，对称轴左边，y随x增大而增大；对称轴右边，y随x增大而减小才能得出正确答案．
