题目内容
【题目】如图,抛物线L:y=ax2+bx+c与x轴交于A、B(3,0)两点(A在B的左侧),与y轴交于点C(0,3),已知对称轴x=1.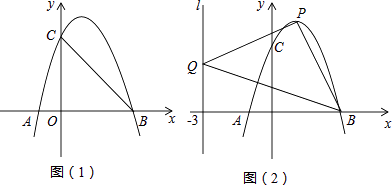
(1)求抛物线L的解析式;
(2)将抛物线L向下平移h个单位长度,使平移后所得抛物线的顶点落在△OBC内(包括△OBC的边界),求h的取值范围;
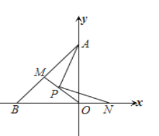
(3)设点P是抛物线L上任一点,点Q在直线l:x=﹣3上,△PBQ能否成为以点P为直角顶点的等腰直角三角形?若能,求出符合条件的点P的坐标;若不能,请说明理由.
【答案】
(1)
解:∵抛物线的对称轴x=1,B(3,0),
∴A(﹣1,0)
∵抛物线y=ax2+bx+c过点C(0,3)
∴当x=0时,c=3.
又∵抛物线y=ax2+bx+c过点A(﹣1,0),B(3,0)
∴ ![]() ,
,
∴ ![]()
∴抛物线的解析式为:y=﹣x2+2x+3
(2)
解:∵C(0,3),B(3,0),
∴直线BC解析式为y=﹣x+3,
∵y=﹣x2+2x+3=﹣(x﹣1)2+4,
∴顶点坐标为(1,4)
∵对于直线BC:y=﹣x+1,当x=1时,y=2;将抛物线L向下平移h个单位长度,
∴当h=2时,抛物线顶点落在BC上;
当h=4时,抛物线顶点落在OB上,
∴将抛物线L向下平移h个单位长度,使平移后所得抛物线的顶点落在△OBC内(包括△OBC的边界),
则2≤h≤4

(3)
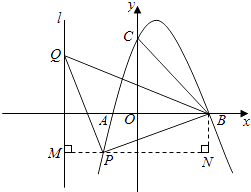
解:设P(m,﹣m2+2m+3),Q(﹣3,n),
①当P点在x轴上方时,过P点作PM垂直于y轴,交y轴与M点,过B点作BN垂直于MP的延长线于N点,如图所示:
∵B(3,0),
∵△PBQ是以点P为直角顶点的等腰直角三角形,
∴∠BPQ=90°,BP=PQ,
则∠PMQ=∠BNP=90°,∠MPQ=∠NBP,
在△PQM和△BPN中,  ,
,
∴△PQM≌△BPN(AAS),
∴PM=BN,
∵PM=BN=﹣m2+2m+3,根据B点坐标可得PN=3﹣m,且PM+PN=6,
∴﹣m2+2m+3+3﹣m=6,
解得:m=1或m=0,
∴P(1,4)或P(0,3).
②当P点在x轴下方时,过P点作PM垂直于l于M点,过B点作BN垂直于MP的延长线于N点,
同理可得△PQM≌△BPN,
∴PM=BN,
∴PM=6﹣(3﹣m)=3+m,BN=m2﹣2m﹣3,
则3+m=m2﹣2m﹣3,
解得m= ![]() 或
或 ![]() .
.
∴P( ![]() ,
, ![]() )或(
)或( ![]() ,
, ![]() ).
).
综上可得,符合条件的点P的坐标是(1,4),(0,3),( ![]() ,
, ![]() )和(
)和( ![]() ,
, ![]() ).
).
【解析】(1)利用待定系数法求出抛物线的解析式即可;(2)先求出直线BC解析式为y=﹣x+3,再求出抛物线顶点坐标,得出当x=1时,y=2;结合抛物线顶点坐即可得出结果;(3)设P(m,﹣m2+2m+3),Q(﹣3,n),由勾股定理得出PB2=(m﹣3)2+(﹣m2+2m+3)2 , PQ2=(m+3)2+(﹣m2+2m+3﹣n)2 , BQ2=n2+36,过P点作PM垂直于y轴,交y轴与M点,过B点作BN垂直于MP的延长线于N点,由AAS证明△PQM≌△BPN,得出MQ=NP,PM=BN,则MQ=﹣m2+2m+3﹣n,PN=3﹣m,得出方程﹣m2+2m+3﹣n=3﹣m,解方程即可.