题目内容
【题目】已知a+b=1,ab=﹣1,设S1=a+b,S2=a2+b2,S3=a3+b3,…,Sn=an+bn
(1)计算S2.
(2)请阅读下面计算S3的过程:
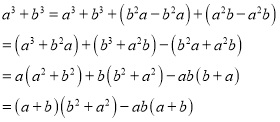
∵a+b=1,ab=﹣1
∴S3=a3+b3=(a+b)(a2+b2)﹣ab(a+b)=1×S2﹣(﹣1)=S2+1= .
你读懂了吗?请你先填空完成(2)中S3的计算结果,再用你学到的方法计算S4
(3)试写出Sn﹣2,Sn﹣1,Sn三者之间的数量关系式(不要求证明,且n是不小于2的自然数),根据得出的数量关系计算S7.
【答案】(1)3;(2)4,S4=7;(3)Sn﹣2+Sn﹣1=Sn,S7=29.
【解析】
(1)根据完全平方公式即可求出S2;
(2)根据得出的结论,代入即可求出S3;根据完全平方公式即可求出S4;
(3)根据(1)(2)求出的结果得出规律,即可求出答案.
解:(1)S2=a2+b2=(a+b)2﹣2ab=12﹣2×(﹣1)=3;
(2)S3=S2+1=3+1=4;
∵S4=a4+b4=( a2+b2)2﹣2a2b2=( a2+b2)2﹣2(ab)2,
又∵a2+b2=3,ab=﹣1,
∴S4=7,
故答案为:4.
(3)∵S1=1,S2=3,S3=4,S4=7,
∴S1+S2=S3,S2+S3=S4.
猜想:Sn﹣2+Sn﹣1=Sn.
∵S3=4,S4=7,
∴S5=S3+S4=4+7=11,
∴S6=S4+S5=7+11=18,
∴S7=S5+S6=11+18=29.

练习册系列答案
 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案
相关题目