ƒøƒ⁄»›
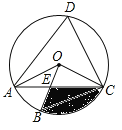
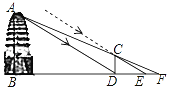
°æƒø°ø»ÁÕº «Œª”⁄…¬Œ˜ °Œ˜∞≤ –ºˆ∏£À¬ƒ⁄µƒ–°—„À˛£¨ «÷–π˙‘Á∆⁄∑Ω–Œ√‹È‹ Ω◊©À˛µƒµ‰–Õ◊˜∆∑£¨≤¢◊˜Œ™Àø≥Ò÷Ƭ∑µƒ“ª¥¶÷ÿ“™“≈÷∑µ„£¨±ª¡–»Î°∂ ¿ΩÁ“≈≤˙√˚¬º°∑£Æ–°√˙°¢–°œ£µ»º∏ŒªÕ¨—ߜο˚”√“ª–©≤‚¡øπ§æfl∫ÕÀ˘—ßµƒº∏∫Œ÷™ ∂≤‚¡ø–°—„À˛µƒ∏fl∂»£¨”…”⁄π€≤‚µ„”Ζ°—„À˛µ◊≤øº‰µƒæ‡¿Î≤ª“◊≤‚¡ø£¨“Ú¥Àæ≠π˝—–æø–Ë“™Ω¯––¡Ω¥Œ≤‚¡ø£¨”⁄ «‘⁄—Ùπ‚œ¬£¨À˚√« ◊œ»¿˚”√”∞≥§Ω¯––≤‚¡ø£¨∑Ω∑®»Áœ¬£∫–°√˙‘⁄–°—„À˛µƒ”∞◊”∂•∂ÀD¥¶ ˙÷±¡¢“ª∏˘ƒæ∞ÙCD£¨≤¢≤‚µ√¥À ±ƒæ∞Ùµƒ”∞≥§DE=2.4√◊£ª»ª∫Û£¨–°œ£‘⁄BDµƒ—”≥§œfl…œ’“≥ˆ“ªµ„F£¨ πµ√A°¢C°¢F»˝µ„‘⁄Õ¨“ª÷±œfl…œ£¨≤¢≤‚µ√DF=2.5√◊£Æ“—÷™Õº÷–À˘”–µ„æ˘‘⁄Õ¨“ª∆Ω√ʃ⁄£¨ƒæ∞Ù∏flCD=1.72√◊£¨AB°ÕBF£¨CD°ÕBF£¨ ‘∏˘æ›“‘…œ≤‚¡ø ˝æ›£¨«Û–°—„À˛µƒ∏fl∂»AB£Æ
°æ¥∞∏°ø43√◊.
°æΩ‚Œˆ°ø
∏˘æ›œ‡À∆»˝Ω«–Œµƒ–‘÷ µ√µΩ![]() =
=![]() =
=![]() £¨µ»¡ø¥˙ªªµ√µΩ
£¨µ»¡ø¥˙ªªµ√µΩ![]() =
=![]() £¨¥˙»Î ˝æ›º¥ø…µ√µΩΩ·¬€£Æ
£¨¥˙»Î ˝æ›º¥ø…µ√µΩΩ·¬€£Æ
”…“‚µ√£∫°œABD=°œCDE=90°„£¨°œADB=°œCED£¨°‡°˜CDE°◊°˜ABD£¨°‡![]() =
=![]() £Æ
£Æ
°fl°œF=°œF£¨°‡°˜CDF°◊°˜ABF£¨°‡![]() =
=![]() £¨°‡
£¨°‡![]() =
=![]() £¨º¥
£¨º¥![]() =
=![]() £¨°‡BD=60£¨°‡
£¨°‡BD=60£¨°‡![]() =
=![]() £¨°‡AB=43£Æ
£¨°‡AB=43£Æ
¥£∫–°—„À˛µƒ∏fl∂»AB «43√◊£Æ

 ≈‡”≈ø⁄À„Âø®œµ¡–¥∞∏
≈‡”≈ø⁄À„Âø®œµ¡–¥∞∏ ø™–ƒø⁄À„Âø®œµ¡–¥∞∏
ø™–ƒø⁄À„Âø®œµ¡–¥∞∏ ø⁄À„Âø®∫”±±…ŸƒÍ∂˘ÕØ≥ˆ∞Ê…Áœµ¡–¥∞∏
ø⁄À„Âø®∫”±±…ŸƒÍ∂˘ÕØ≥ˆ∞Ê…Áœµ¡–¥∞∏°æƒø°ø“ª∏ˆΩ Ù∞Ù‘⁄≤ªÕ¨Œ¬∂»œ¬£¨∆‰≥§∂»“≤≤ªÕ¨£¨∆‰±‰ªØ«Èøˆ»Áœ¬±Ì£∫
Œ¬∂»/°Ê | °≠ | -5 | 0 | 5 | 10 | 15 | °≠ |
≥§∂»/ | °≠ | 13.9 | 13.95 | 14 | 14.05 | 14.1 | °≠ |
£®1£©…œ ˆ¡Ω∏ˆ±‰¡ø÷–£¨◊‘±‰¡ø « £ª
£®2£©…Ë◊‘±‰¡øŒ™![]() £¨“Ú±‰¡øŒ™
£¨“Ú±‰¡øŒ™![]() £¨«Û≥ˆ
£¨«Û≥ˆ![]() πÿ”⁄
πÿ”⁄![]() µƒΩ‚Œˆ Ω£ª
µƒΩ‚Œˆ Ω£ª
£®3£©µ±Œ¬∂»Œ™30°Ê ±£¨«ÛΩ Ù∞Ùµƒ≥§∂»£ª
£®4£©»Ùƒ≥ÃÏΩ Ù∞Ùµƒ≥§∂» «14.18![]() £¨‘Úµ±Ãϵƒ∆¯Œ¬‘º «∂‡…Ÿ°Ê£ø
£¨‘Úµ±Ãϵƒ∆¯Œ¬‘º «∂‡…Ÿ°Ê£ø
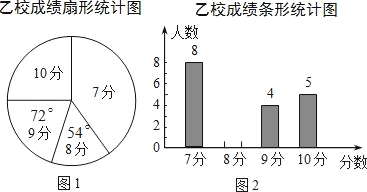
°æƒø°ø£®10∑÷£©º◊°¢““¡Ω–£≤Œº” –ΩÔ˝æ÷æŸ∞ϵƒ≥ı÷–…˙”¢”Ôø⁄”Ôæ∫»¸£¨¡Ω–£≤Œ»¸»À ˝œ‡µ»£Æ±»»¸Ω· ¯∫Û£¨∑¢œ÷—ß…˙≥…º®∑÷±Œ™7∑÷°¢8∑÷°¢9∑÷°¢10∑÷£®¬˙∑÷Œ™10∑÷£©£Æ“¿æ›Õ≥º∆ ˝æ›ªÊ÷∆¡À»Áœ¬…–≤ªÕÍ’˚µƒÕ≥º∆Õº±Ì£Æ
∑÷ ˝ | 7∑÷ | 8∑÷ | 9∑÷ | 10∑÷ |
»À ˝ | 11 | 0 | °° °° | 8 |
£®1£©«ÎΩ´º◊–£≥…º®Õ≥º∆±Ì∫ÕÕº2µƒÕ≥º∆Õº≤π≥‰ÕÍ’˚£ª
£®2£©æ≠º∆À„£¨““–£µƒ∆Ωæ˘∑÷ «8.3∑÷£¨÷–Œª ˝ «8∑÷£¨«Î–¥≥ˆº◊–£µƒ∆Ωæ˘∑÷°¢÷–Œª ˝£ª≤¢¥”∆Ωæ˘∑÷∫Õ÷–Œª ˝µƒΩ«∂»∑÷Œˆƒƒ∏ˆ—ß–£≥…º®Ωœ∫√£Æ