题目内容
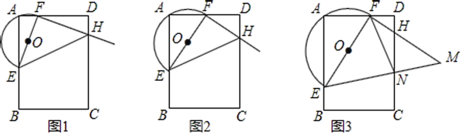
【题目】已知:在矩形ABCD中,E,F分别是边AB,AD上的点,过点F作EF的垂线交DC于点H,以EF为直径作半圆O.
(1)填空:点A (填“在”或“不在”)⊙O上;当弦AE等于弦AF时,![]() 的值是 ;
的值是 ;
(2)如图1,在△EFH中,当FE=FH时,求证:AD=AE+DH;
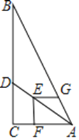
(3)如图2,当△EFH的顶点F是边AD的中点时,求证:EH=AE+DH;
(4)如图3,点M在线段FH的延长线上,若FM=FE,连接EM交DC于点N,连接FN,当AE=AD时,FN=4,HN=3,直接写出![]() 的值.
的值.
【答案】(1)在,1;(2)证明见解析;(3)证明见解析;(4)![]()
【解析】
(1)连接AO,∠EAF=90°,O为EF中点,所以AO=![]() EF,因此点A在⊙O上,当弦AE等于弦AF时,∠AEF=45°,tanAEF=tan45°=
EF,因此点A在⊙O上,当弦AE等于弦AF时,∠AEF=45°,tanAEF=tan45°=![]() =1;
=1;
(2)证明△AEF≌△DFH(AAS),得到AF=DH,AE=DF,所以AD=AF+DF=AE+DH;
(3)延长EF交HD的延长线于点G,先证明△AEF≌△DGF(ASA),所以AE=DG,EF=FG,因为EF⊥FG,所以EH=GH,GH=DH+DG=DH+AE,即EH=AE+DH;
(4)过点M作MQ⊥AD于点Q,设AF=x,AE=a,所以△EFM是等腰直角三角形,∠FEM=∠FMN=45°,因此△AEF≌△QFM(ASA),AE=EQ=a,AF=QM,AE=AD,AF=DQ=QM,由△FEN∽△HMN,得到![]() ,所以tanAEF=
,所以tanAEF=![]() =
=![]() .
.
(1)连接AO,如图1所示:
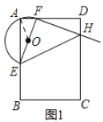
∵∠EAF=90°,O为EF中点,
∴AO=![]() EF,
EF,
∴点A在⊙O上,
当弦AE等于弦AF时,∠AEF=45°,
∴tanAEF=tan45°=![]() =1.
=1.
故点A在⊙O上;当弦AE等于弦AF时,![]() 的值是1.
的值是1.
(2)∵EF⊥FH,
∴∠EFH=90°,
在矩形ABCD中,∠A=∠D=90°,
∴∠AEF+∠AFE=90°,∠AFE+∠DFH=90°,
∴∠AEF=∠DFH,
又FE=FH,
∴△AEF≌△DFH(AAS),
∴AF=DH,AE=DF,
∴AD=AF+DF=AE+DH;
(3)如图2所示,延长EF交HD的延长线于点G,
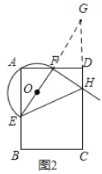
∵F分别是边AD上的中点,
∴AF=DF,
∵∠A=∠FDG=90°,∠AFE=∠DFG,
∴△AEF≌△DGF(ASA),
∴AE=DG,EF=FG,
∵EF⊥FG,
∴EH=GH,
∴GH=DH+DG=DH+AE,
∴EH=AE+DH;
(4)过点M作MQ⊥AD于点Q,如图3所示,
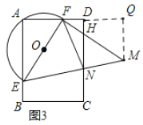
设AF=x,AE=a,
∵FM=FE,EF⊥FH,
∴△EFM是等腰直角三角形,
∴∠FEM=∠FMN=45°,
∵FM=FE,
∠A=∠MQF=90°,
∠AEF=∠MFQ,
∴△AEF≌△QFM(ASA),
∴AE=EQ=a,AF=QM,
∵AE=AD,
∴AF=DQ=QM=x,
∵DC![]() QM,
QM,
∴![]() ,
,
∵DC![]() AB
AB![]() QM,
QM,
∴![]() ,
,
∴![]() ,
,
∵FE=FM,
![]() ,
,
∠FEM=∠FMN=45°,
∴△FEN∽△HMN,
∴![]() ,
,
∴tanAEF=![]() =
=![]() .
.

【题目】已知抛物线![]()
![]() 对称轴为______,顶点坐标为______;
对称轴为______,顶点坐标为______;
![]() 在坐标系中利用五点法画出此抛物线.
在坐标系中利用五点法画出此抛物线.
x |
| ______ | ______ | ______ | ______ | ______ |
|
y |
| ______ | ______ | ______ | ______ | ______ |
|
![]() 若抛物线与x轴交点为A、B,点
若抛物线与x轴交点为A、B,点![]() 在抛物线上,求
在抛物线上,求![]() 的面积.
的面积.