题目内容
【题目】已知:如图,△ABC是等边三角形,点D、E分别在边BC、AC上,且BD=CE,AD与BE相交于点F.
(1)求证:△ABD≌△BCE
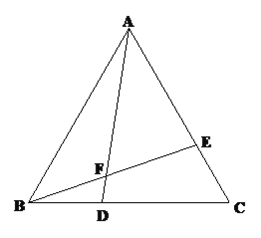
(2)求证: ![]()
【答案】(1)证明见解析;(2)证明见解析
【解析】试题分析:
(1) 要证△ABD≌△BCE,利用△ABC是等边三角形可以得到,AB=BC,∠ABC=∠BCA. 在这种情况下观察图形可知,在待证明的两个三角形中已经获得一组对应边相等和一组对应角相等,再根据已知条件BD=CE,根据SAS即可证明这两个三角形全等.
(2) 观察待证明的等式形式可知,AE应为BE和EF的比例中项. 将待证明的等式改写为比例式后,利用“三点定形法”可以找到一组合适的相似三角形△EBA与△EAF. 观察这两个三角形发现:这两个三角形有一组对应角为公共角;对于另一组对应角∠EBA与∠EAF而言,可以通过第(1)问中的全等三角形和△ABC的性质证明其相等. 利用相似三角形的判定定理即可获得这组三角形相似,进而证明等式成立.
试题解析:
(1) ∵△ABC是等边三角形,
∴AB=BC,∠ABC=∠BCA,即∠ABD=∠BCE,
∵在△ABD与△BCE中:
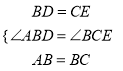 ,
,
∴△ABD≌△BCE (SAS).
(2) ∵△ABC是等边三角形,
∴∠ABC=∠BAC,
∵△ABD≌△BCE,
∴∠BAD=∠CBE,
∴∠ABC-∠CBE =∠BAC-∠BAD,
∴∠EBA=∠CAD,即∠EBA=∠EAF,
∵在△EBA与△EAF中:
∠AEB=∠FEA (公共角),∠EBA=∠EAF,
∴△EBA∽△EAF,
∴![]() ,
,
即AE2=BE·EF.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目