题目内容
【题目】如图,Rt△ABC中,∠ACB=90°,以AC为直径的⊙O交AB于点D,过点D作⊙O的切线交BC于点E,连接OE
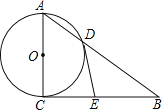
(1)求证:△DBE是等腰三角形
(2)求证:△COE∽△CAB
【答案】(1)见解析;(2)见解析
【解析】
(1)连接OD,由DE是⊙O的切线,得出∠ODE=90°,∠ADO+∠BDE=90°,由∠ACB=90°,得出∠CAB+∠CBA=90°,证出∠CAB=∠ADO,得出∠BDE=∠CBA,即可得出结论;
(2)证出CB是⊙O的切线,得出DE=EC,推出EC=EB,再由OA=OC,得出OE∥AB,即可得出结论.
(1)连接OD、OE,如图所示:
∵DE是⊙O的切线,
∴∠ODE=90°,
∴∠ADO+∠BDE=90°,
∵∠ACB=90°,
∴∠CAB+∠CBA=90°,
∵OA=OD,
∴∠CAB=∠ADO,
∴∠BDE=∠CBA,
∴EB=ED,
∴△DBE是等腰三角形;
(2)∵∠ACB=90°,AC是⊙O的直径,
∴CB是⊙O的切线,
∵DE是⊙O的切线,
∴DE=EC,
∵EB=ED,
∴EC=EB,
∵OA=OC,
∴OE∥AB,
∴△COE∽△CAB.


练习册系列答案
相关题目